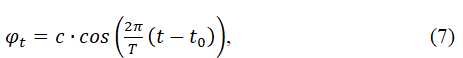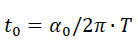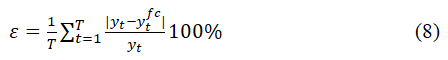УДК 336.02
DOI 10.24412/2413-046Х-2021-10434
Выбор спецификации тренд – сезонной модели прогнозирования стоимости товара
Selection of the specification of a trend-seasonal model for forecasting the cost of goods
Чесноков Евгений Александрович, кандидат физико – математических наук, доцент, Санкт – Петербургский государственный университет аэрокосмического приборостроения
Chesnokov Evgeny Alexandrovich, PhD of Physico – mathematical Sciences, Associate Professor, St. Petersburg State University of Aerospace Instrumentation, E-mail: eachesn@yandex.ru
Аннотация. Статья посвящена анализу различных тренд – сезонных моделей прогнозирования стоимости товара. На основании использования различных статистик проведено комплексное сравнение моделей как с точки зрения удобства использования и простоты интерпретации результатов, так и с точки зрения точности получаемых по ним прогнозов. Особое внимание уделено выбору способа выделения тренда, а также идентификации сезонных колебаний малой амплитуды. Полученные результаты в равной мере могут быть использованы для прогнозирования объемов продаж или объемов выпуска продукции по данным временных рядов.
Summary. The article is devoted to the analysis of various trend-seasonal models for forecasting the cost of goods. Using various statistics, a comprehensive comparison of models was carried out taking into account both the convenience of use and the clarity of interpretation of the results, and the accuracy of the forecasts obtained from them. Special attention is paid to the choice of the method for selecting the trend, as well as identifying seasonal small amplitude fluctuations. The results obtained can equally be used to predict sales volumes or output volumes based on time series data.
Ключевые слова: временной ряд, прогнозирование, регрессия, тренд – сезонная модель, гармонический ряд, коэффициент сезонности.
Keywords: time series, forecasting, regression, trend-seasonal model, harmonic series, seasonality coefficient.
- Введение
Прогноз стоимости товара, объема продаж или объема производимой продукции являются важными составляющими при планировании деятельности различных организаций. Особую актуальность прогнозирование стоимости товаров с ярко выраженными сезонными колебаниями традиционно представляет для торговых организаций и предприятий аграрно-промышленного комплекса. Один из основных способов получения прогноза состоит в анализе временных рядов, сформированных для интересующей нас переменной по данным за некоторый предшествующий интервал времени.
С развитием компьютерных технологий и появлением ряда мощных статистических пакетов (Statistica, STATA, EViews и др.) стало возможным практическое использование различных моделей временных рядов: авторегрессионные модели, модели скользящей средней, ARMA, ARIMA и другие. В то же время, неизменно популярными остаются и классические регрессионные модели, основанные на выделении объективно-обусловленной (детерминированной) составляющей временного ряда (смотри, например, [1-8]). Последняя, в свою очередь, может быть разделена на трендовую, циклическую и сезонную компоненты. Трендовая, плавно меняющаяся часть временного ряда, отвечает за описание монотонных экономических процессов, таких как увеличение объема выпуска продукции в результате роста уровня технологий или же монотонный рост цен, вызванный инфляционными процессами. Для циклической составляющей характерны многолетние периоды экономической активности. Сезонная составляющая имеет годовой период колебаний экономического показателя.
Популярность классических регрессионных моделей обусловлена в первую очередь простотой интерпретации получаемых результатов, а также минимумом программного обеспечения, необходимого для их использования. Во многих случаях оказывается достаточным статистического пакета EXCEL (смотри, например, [4]).
Построение тренд – сезонных моделей осуществляется, как правило, в два этапа. На первом этапе выделяется тренд и формируется детрендированный (с исключенным трендом) временной ряд. Здесь возможны два основных подхода: аддитивный (тренд вычитается из исходных значений ряда) и мультипликативный (исходный ряд делится на тренд). Аддитивные модели более просты математически, что особенно важно при построении доверительных интервалов (смотри, например, [5]). С другой стороны, более естественным представляется использование мультипликативных моделей (смотри, например, [7]), в которых сезонные колебания определяются в процентах от среднегодового значения рассматриваемой величины, а не в абсолютных размерных значениях, как это имеет место в случае аддитивных моделей. Руководствуясь указанными соображениями, авторы различных работ в равной степени используют как аддитивные, так и мультипликативные модели. В то же время, сколько-нибудь подробного сравнительного анализа аддитивных и мультипликативных моделей на предмет их точности, насколько известно автору настоящей работы, до сих пор не проводилось.
На втором этапе, при построении тренд – сезонной модели, детрендированный ряд подвергается анализу на предмет наличия сезонных колебаний и выделяется сезонная составляющая ряда. Здесь также практикуются два подхода. Первый состоит в использовании ежемесячных или ежеквартальных коэффициентов сезонности, представляющих собой среднемесячные или среднеквартальные абсолютные (для аддитивных моделей) или относительные (для мультипликативных моделей) отклонения исследуемой величины от среднегодового значения (смотри, например, [1-2,8]). Второй подход основан на разложении периодической сезонной компоненты в дискретный ряд Фурье (смотри, например, [3-7]). Оба подхода, при сохранении всех членов ряда, обеспечивают одинаковую точность аппроксимации статистических данных.
Зачастую предпочтение отдается первому подходу из-за простоты интерпретации параметров (коэффициентов сезонности). В то же время, в большинстве случаев хороший прогноз можно получить, сохраняя только первую гармонику в ряде Фурье. При этом, как будет показано дальше, второй подход позволяет дать еще более наглядную интерпретацию параметров.
Следует отметить, что большинство работ посвящено исследованию экономических показателей, заведомо имеющих ярко выраженную сезонную составляющую. Например, в работах [6-8] приводятся прогнозы цен на различные виды сельскохозяйственной продукции. В таких случаях не возникает вопроса о значимости сезонных колебаний. В то же время, вопрос о наличии значимых сезонных колебаний далеко не всегда представляется очевидным. Выявление сезонных колебаний малой амплитуды путем сравнения различных статистик также является одной из задач настоящей работы.
- Описание тренд – сезонных моделей
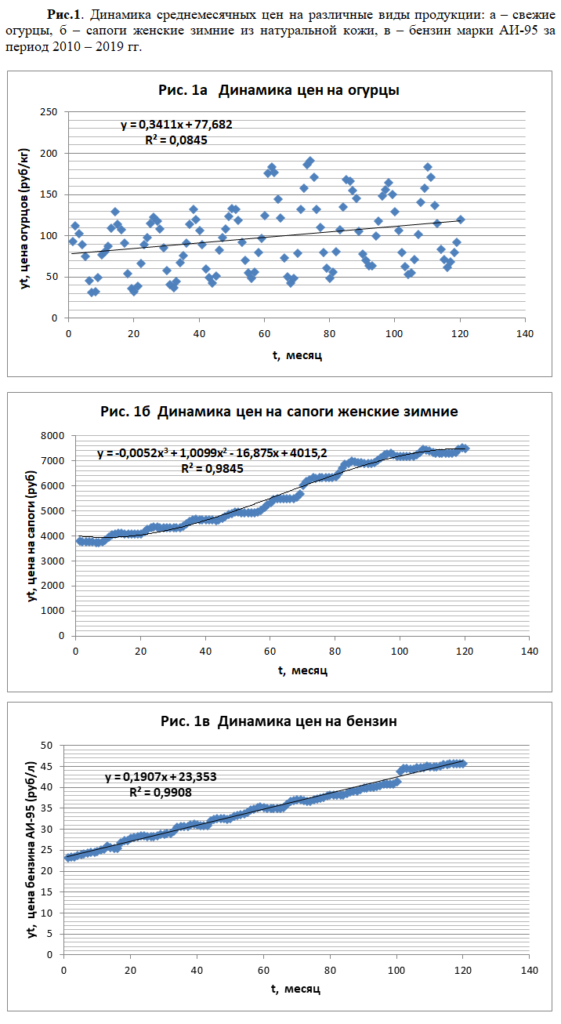
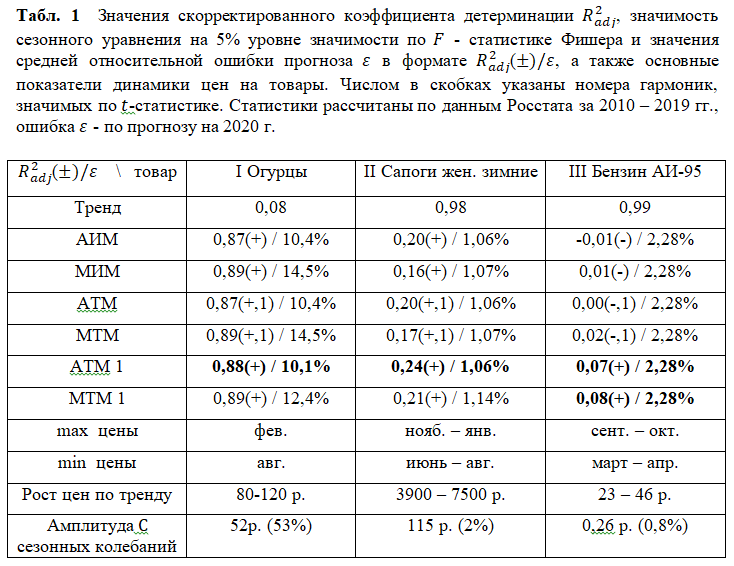
Тренд – сезонные экономические модели предполагают учет монотонного изменения экономического показателя во времени (тренда) одновременно с его сезонными периодическими изменениями. В случае прогноза стоимости товара тренд обусловлен, как правило, монотонным ростом цен по причине инфляции или же монотонным ростом (падением) спроса при вводе или выходе некоторого вида товара из употребления. Сезонная составляющая связана с сезонными колебаниями спроса или объема выпуска товара. В зависимости от вида товара, а также от множества влияющих на его производство и спрос экономических факторов, динамика цен на товар может иметь более или менее ярко выраженные трендовую и сезонную компоненты. На рис. 1 приведена динамика цен на различные виды товаров за период 2010 – 2019 гг.
Наряду с уравнением регрессии, параметры которого оценены по методу наименьших квадратов, и линией тренда, на каждом рисунке приведено значение коэффициента детерминации , показывающее в какой доле изменение стоимости товара за весь период учитывается в рамках предложенного тренда.
Как видно из рис. 1а, цены на огурцы, как и следовало ожидать, имеют ярко выраженные сезонные колебания, заметно превосходящие по амплитуде монотонный рост цен, определяемый линией тренда. Согласно коэффициенту детерминации, в случае огурцов трендовый рост объясняет лишь 8% от общей вариации цен.
Полную противоположность демонстрируют собой цены на бензин (рис. 1в). Здесь вариация цен за рассмотренный временной интервал на 99% воспроизводится линейным трендом, в то время как наличие периодических сезонных колебаний представляется весьма неоднозначным.
Динамика цен на сапоги (рис. 1б) демонстрирует промежуточный вариант ценообразования. Напряду с ярко выраженным трендом, который на 98% объясняет вариацию цен, имеют место и хорошо наблюдаемые на диаграмме периодические сезонные колебания, амплитуда которых, тем не менее, мала в сравнении с монотонным возрастанием цены за весь период. Отметим, что для случая, приведенного на рис. 1б, характерно изменение скорости монотонного роста. Линейная зависимость оказывается при этом малоподходящей, и предпочтение было отдано кубической спецификации тренда.
После получения уравнения тренда ft, формируется детрендированный ряд.
В случае аддитивной модели, задаваемой уравнением
где ft – тренд, φt – сезонная детерминированная компонента, єt – случайная составляющая ряда, детрендированный ряд получается простым вычитанием тренда
Для случая мультипликативной модели, задаваемой уравнением
очистка от тренда выполняется по формуле
Если монотонно растущий тренд интерпретировать как среднегодовую цену, то сезонная компонента φt представляет собой среднемесячное отклонение цены в месяце от среднегодовой для аддитивной модели и среднемесячное относительное отклонение цены от среднегодовой для мультипликативной модели. Как правило, для растущего тренда, предпочтение мультипликативной модели отдают при наличии визуально наблюдаемого роста амплитуды сезонных колебаний от года к году. Для малых амплитуд сезонных колебаний (рис. 1б,в) такой подход оказывается неприменимым. Для случая, изображенного на рис. 1а, возможно говорить о визуальном увеличении амплитуды сезонных колебаний во второй половине рассмотренного временного интервала, однако, связано это увеличение, по-видимому, с кризисом цен 2014 г., который, в свою очередь, не может быть учтен в рамках плавной монотонной спецификации тренда.
Во всех перечисленных случаях для выбора аддитивной или мультипликативной спецификации тренд – сезонной модели, а также для идентификации сезонных колебаний малой амплитуды, можно предложить следующий подход. Для детрендированных рядов, полученных в рамках аддитивного и мультипликативного подходов, строится вторая регрессия по факторам сезонности. Далее рассматриваются показатели качества построенных регрессий. Значимость уравнения в целом по F – статистике Фишера (pF<0,05), а также значимость хотя бы одного из параметров по t – статистике (pyk<0,05 или paj<0,05 или pbj<0,05) свидетельствуют о значимости (доказывают наличие) сезонных колебаний. Сравнение различных значимых моделей между собой может быть выполнено на основе рассмотрения скорректированного коэффициента детерминации R2adj. При прочих равных условиях предпочтение следует отдавать модели с наибольшим значением R2adj.
В зависимости от используемого набора факторов сезонности различают индикаторные и тригонометрические модели (смотри, например, [9]).
Спецификация индикаторной модели имеет вид
где ytk – индикатор месяца (квартала), равный единице, если месяц (квартал) t имеет порядковый номер k в году и нулю во всех остальных случаях, T- период сезонных колебаний (T=12 для ежемесячных данных и T=4 для ежеквартальных). Параметры yk, оцениваемые по методу наименьших квадратов, носят название коэффициентов сезонности и представляют собой среднемесячные (для аддитивных моделей с ежемесячными данными) и среднемесячные относительные (для мультипликативных моделей) отклонения цены от среднегодовой. Простота интерпретации параметров является несомненным преимуществом индикаторных моделей.
Спецификация тригонометрической модели задается уравнением
где j – порядковый номер гармоники тригонометрического ряда.
В зависимости от выбора способа выделения тренда (аддитивный или мультипликативный) и выбора спецификации сезонной компоненты (индикаторная или тригонометрическая), можно выделить четыре класса тренд – сезонных моделей:
АИМ – аддитивная индикаторная модель,
МИМ – мультипликативная индикаторная модель,
АТМ – аддитивная тригонометрическая модель и
МТМ – мультипликативная тригонометрическая модель.
Хотя точность аппроксимации дискретных рядов на основе моделей (5) и (6) одинакова, интерпретация параметров в тригонометрических моделях (6) весьма затруднена. Исключение составляет наиболее часто встречающаяся ситуация, когда значимость первой гармоники (значимость параметров a1 или b1 по t – статистике) намного превосходит (p – значение намного меньше) значимость остальных гармоник. В этом случае допустимо без существенной потери точности ограничиться одной гармоникой и перейти к спецификации
параметры которой имеют предельно ясную интерпретацию.
Здесь
– амплитуда сезонных колебаний,
– порядковый номер месяца в году, на который приходится максимум цены товара. Отметим, что минимум цены, в рамках приближения (7), достигается ровно через полгода. Фаза a0 задается уравнением
a0=arcos(a1/c), если b1≥0 и уравнением
a0=2π – arcos(a1/c), если b1<0.
Модели вида (7), с одной гармоникой, мы будем обозначать АТМ1 и МТМ1 в случаях аддитивной и мультипликативной спецификаций соответственно.
Отметим, что как в случае индикаторных моделей, так и в случае тригонометрических, все сезонные факторы являются ортогональными, так что удаление из ряда любого числа незначимых факторов никак не влияет на точность оценки параметров при оставшихся факторах.
3. Сравнение результатов
В соответствии с подходом, изложенным в предыдущем разделе, в табл. 1 приведены значения скорректированного коэффициента детерминации R2adj, а также отмечена значимость сезонных уравнений регрессии по F – статистике Фишера для сравнительного анализа качества различных тренд – сезонных моделей.
Для непосредственной оценки точности прогноза по каждой модели приведены значения средней относительной ошибки є, рассчитанные по формуле
по данным цен yt на 2020 г., yfct – прогнозные значения по модели.
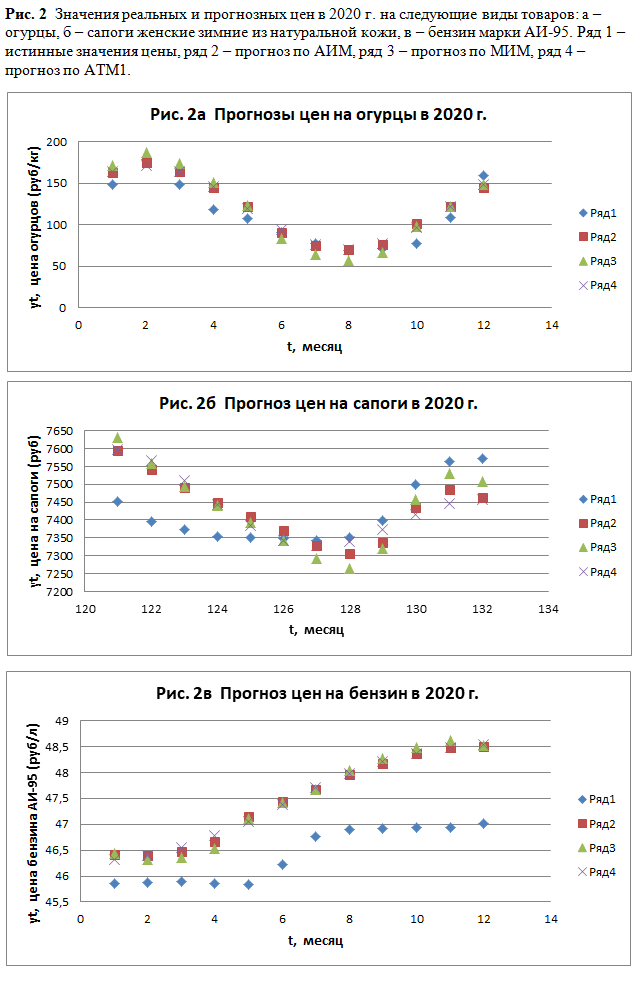
Для большей наглядности и лучшего понимания результатов на рис. 2 приведены диаграммы сравнения реальных цен на товары в 2020 г. и их прогнозные значения, полученные по различным моделям на основании данных за предшествующие 10 лет.
Для товара с ярко выраженной сезонностью (огурцы, рис. 1а, 2а) АТМ1 оказалась как наиболее простой, так и наиболее точной, несмотря на более высокое значение R2adj для мультипликативных моделей. Мультипликативные модели демонстрируют завышенную амплитуду сезонных колебаний, что связано с непрогнозируемым ростом амплитуды в результате кризиса цен 2014 г. При прогнозировании по всем моделям максимум цен приходится на февраль, минимум – на август. Амплитуда сезонных колебаний цен по АТМ1 составляет 52 рубля или 53% от среднегодовой цены товара.
Для товара с хорошо выраженным трендом и малой амплитудой сезонных колебаний (сапоги, рис. 1б, 2б) АТМ1 также оказалась наилучшей. Мультипликативные модели уступают в точности прогноза, по-видимому, по причине несколько искусственной (обусловленной подбором наилучшей аппроксимации, а не объективными соображениями) кубической спецификации тренда. По результатам различных моделей, максимум цены приходится на ноябрь – январь, минимум – на июнь – август каждого года. Согласно АТМ1 амплитуда сезонных колебаний составляет 115 рублей или 2% от стоимости товара.
Наибольший интерес представляют результаты анализа цен на бензин (рис. 1в, 2в). АТМ1 и МТМ1 в равной степени демонстрируют как наилучшую аппроксимацию данных, на основе которых они были оценены (сравнение по R2adj), так и наилучшую точность прогноза на следующий год (сравнение по ). Значимость сезонных колебаний удается установить только на основе рассмотрения тригонометрических моделей сезонности. Особенно четко она проявляется в коротких АТМ1 и МТМ1 моделях, значимых не только по t – статистике коэффициентов, но и по F – статистике Фишера. Несмотря на четко выраженный тренд, мультипликативные модели не имеют преимущества над аддитивными. Все тренд – сезонные модели прогнозируют завышенное среднегодовое значения цены на бензин, что обусловлено снижением роста цены в силу влияния трудно учитываемых факторов, но корректно воспроизводят заметный рост цен в летний период. Максимум цен приходится на сентябрь – октябрь, минимум – на март – апрель каждого года.
Отметим, что выявленные сезонные колебания цен на бензин составляют лишь 0,26 рубля по амплитуде или 0,8% от среднегодовой цены товара. Выявленные колебания подтверждаются сравнением реальных цен с прогнозными, что свидетельствует о возможности корректного учета сезонных колебаний малой амплитуды на фоне ярко выраженного тренда, по крайней мере, по тригонометрическим моделям.
4. Заключение
В заключении приведем ряд качественных выводов, которые могут быть сделаны по результатам проведенного анализа.
Использование мультипликативных моделей при анализе сезонных колебаний стоимости товара представляется наиболее естественным, поскольку подорожания и скидки происходят, как правило, в процентном отношении к предыдущей стоимости товара, а не в абсолютном денежном эквиваленте. Действительно, во многих случаях аппроксимация динамики цены товара мультипликативными моделями дает лучшее качество подгонки. Однако, далеко не всегда прогноз по мультипликативным моделям обеспечивает большую точность. Для хорошей точности прогноза по мультипликативным моделям необходимо наличие хорошо детерминированного тренда. В случаях же, когда тренд слабо выражен, спецификация его вызывает сомнения или же присутствуют некоторые структурные изменения экономической ситуации во времени, точность прогноза по мультипликативным моделям может оказаться заниженной и предпочтение следует отдавать аддитивным моделям. Исключение составляет случай, когда для предварительных прогнозов, в целях экономии времени, мы сразу хотим получить численные значения амплитуды сезонных колебаний в процентном отношении к среднегодовой цене.
Тригонометрические модели в большинстве случаев являются более удобными в сравнении с индикаторными. В случае невырожденных сезонных колебаний малой амплитуды использование тригонометрических моделей, особенно моделей с одной гармоникой, позволяет установить значимость сезонных колебаний, в то время как все коэффициенты сезонности могут оказаться незначимыми. В случае хорошо выраженных сезонных колебаний, близких по форме к синусоиде, как правило, можно ограничиться приближением тригонометрической модели с одной гармоникой, параметры которой C и t0 сразу же определяют амплитуду сезонных колебаний, точки максимума и минимума цен.
Подводя итог вышесказанному, можно рекомендовать следующий алгоритм построения классической тренд – сезонной модели.
На первом шаге визуально анализируется диаграмма динамики цен и подбирается спецификация тренда. Если тренд четко выражен, имеет хорошо объяснимую с экономической точки зрения спецификацию, и отсутствуют структурные изменения в характере временного ряда, при этом амплитуда сезонных колебаний монотонно меняется от начала к концу интервала, следует выбирать мультипликативный способ исключения тренда. Аналогично поступаем в случае, когда мы заинтересованы в наискорейшем получении модели, коэффициенты которой показывают величину сезонных колебаний сразу же в процентном отношении. В остальных случаях тренд исключается аддитивным образом.
Если сезонные колебания на диаграмме ярко выражены, но имеют форму, далекую от синусоиды, выбирается индикаторная модель сезонности, что сразу же позволяет получить оцененные на значимом уровне коэффициенты сезонности. В противном случае оценивается тригонометрическая модель со всеми гармониками. Если значима только первая гармоника или значимость ее заметно превосходит остальные ( – значения гораздо меньше), окончательно переходим к тригонометрической модели с одной гармоникой.
Отметим также, что все вышесказанное в равной мере относится к ежеквартальным временным рядам, однако гармонический характер сезонных колебаний прослеживается в этом случае менее четко.
Список литературы
- Попова Е.В., Кочкарова П.А., Савинская Д.Н., Недогонова Т.А. Тренд – сезонные временные ряды: особенности выявления и прогнозирования // Вестник АГУ, серия «Экономика». – 2019. – Вып.3(245). – С.103 – 109.
- Магомедова Е.С., Османова П.Х. Исследование тренд – сезонных экономических процессов // Вестник Дагестанского государственного университета. – 2008. – Вып.1. – С.23 – 31.
- Протасов Ю.М., Юров В.М. Сравнительная оценка способов моделирования экономических временных рядов с периодическими колебаниями // Вопросы региональной экономики. – 2017. – №2(31)ю – С.181 – 187.
- Юров В.М. Технология прогнозирования периодических экономических процессов на основе методов гармонического анализа в MS EXCEL // Вестник Московского государственного областного университета. Серия: Экономика. – 2018. – №3. – С.19 – 28.
- Юров В.М. Определение доверительных интервалов при прогнозировании тренд – периодических экономических процессов с использованием методов гармонического анализа // Вестник Московского государственного областного университета. Серия: Экономика. – 2019. – №4. – С.89 – 97.
- Бузина Т.С., Полковская М.Н. Моделирование производства аграрной продукции с учетом сезонности цен // Экономика. Информатика. – 2020. – Т.47. – №1. – С.117 – 125.
- Зоркальцев В.И., Полковская М.Н. Аддитивная и мультипликативная модели выявления тренда в сезонных колебаниях: приложение мультипликативной модели к динамике цен на сельскохозяйственную продукцию // Управление большими системами. – 2020. – №86. – С.98 – 115.
- Бурда А.Г., Бурда С.А. Исследование сезонности цен и объемов производства молока на Кубани // Вестник Академии знаний. – 2020. – №38(3). – С.62 – 69.
- Колемаев В.А. Эконометрика: М.: ИНФРА-М, 2006. – 160с.