УДК 517.929; 517.67

DOI 10.24411/2413-046Х-2018-15112

Севодин М.А., к.ф.-м.н., доцент, Пермский национальный исследовательский политехнический университет

Соколов В.А., к.ф.-м.н., доцент, Пермский национальный исследовательский политехнический университет

Sevodin M.A., Sokolov V.A.

О НЕЧЕТКОЙ МОДЕЛИ ВАЛЬРАСА РЫНКА ОДНОГО ТОВАРА

ON FUZZY MODEL OF WALRUS MARKET ONE PRODUCT

Аннотация. В статье рассмотрены хозяйственные субъекты экономики с нечеткими характеристиками.  На основе некоторых нечетких оценок рынка изучена функция избыточного спроса. Представлена модификация  динамической модели Вальраса рынка одного товара. На основе этого и известной ранее четкой модели получены оценки интервального типа положения равновесия указанной модели. Для положения равновесия установлены условия его устойчивости. Они представлены в виде системы неравенств для параметров модели. Кроме того, доказана эквивалентность разрешимости некоторой краевой задачи и классической динамической модели Вальраса рынка одного товара. В последней при этом считается, что с постоянными коэффициенты подстройки цены предложения постоянны, а цена спроса  берется с учетом кусочно-постоянного запаздывания цены предложения. Построено приближенное решение указанной краевой задачи. Результаты, связанные с эквивалентностью краевой задачи и модели рынка, перенесены на случай модифицированной модели интервального типа. Поставлена и решена задача об — кратном изменении цены товара к указанному моменту времени.

Abstract. The article focuses on economic operators with fuzzy properties. Based on some fuzzy market evaluations, the excess demand function is analyzed. A modification of the Walrasian dynamic model of a single commodity market is presented. Based on this and the predefined clear model, interval estimations of the equilibrium point for the model in question are derived. For the equilibrium point, the conditions of its stability are determined. They are represented as a system of inequalities for the model’s parameters. Additionally, the equality is proved between the solvability of some boundary value problem and the classic Walrasian dynamic model of a single commodity market. In the latter, supply price adjustment coefficients are considered constant for constants, while demand price is derived with the piecewise constant lag of supply price taken into consideration. An approximate solution to the aforementioned boundary value problem is presented. The results concerning the equality between the boundary value problem and the market model are applied to the modified interval model. The problem of the w-fold change in commodity price by the specified moment is formulated and solved.

Ключевые слова. Рынок одного товара, положение равновесия, функция спроса, краевая задача, оценки интервального характера.

Keywords. Single commodity market, equilibrium point, demand function, boundary value problem, interval estimations.

   Введение. Дифференциальные уравнения с отклоняющимся аргументом выделяется среди других уравнений своей ориентацией на приложения. Они описывают большое число ситуаций, связанных с прикладными вопросами [1]. В экономике такие уравнения встречаются, например, при моделировании экономики производства, ценообразования, взаимодействия плановых рыночных механизмов и т.д.. Особое место здесь занимает изучение линейных дифференциальных уравнений с запаздывающим аргументом методами функционального анализа [1,2]. Такой подход позволил исследовать на устойчивость различные модификации моделей экономики и установить некоторые параметры этих моделей.

   В то же время всякий экономический процесс протекает в условиях неопределенности, которая порождается большим количеством факторов. В работе [3], например, указывается, что неопределенность, неполнота являются фундаментальными свойствами экономических процессов. Поэтому важно распространить названные выше методы на случай экономических моделей с элементами неопределенности различного типа.

   В данной статье рассматривается модель Вальраса стабилизации цен на рынке одного товара, которая в детерминированной постановке относится к числу классических задач [4-6]. Новые аспекты в ее трактовке и определении равновесия, не укладывающиеся в рамки традиционной теории, возникают при нечеткой интервальной неопределенности коэффициентов и функций, входящих в данную модель. Источниками интервальности здесь являются  неполнота знаний об объекте, ошибки моделирования, погрешности вычисления параметров модели или последствия линеаризации функций спроса и предложения.

   Возможные множества реализаций параметров модели в интервалах задания являются главным отличием интервальной задачи от детерминированной. Вместе с тем небольшое количество информации о действительных значениях коэффициентов не позволяет считать ее стахастической и использовать известные методы фильтрации [7].

   В настоящее время разработана методология решения подобных задач с помощью методов теории нечетких множеств. Математический фундамент нечетких методов исследования в основном был заложен  во второй половине 20 века [8-10].

   Одним из эффективных инструментов исследования различных математических моделей в условиях неопределенности является интервальный анализ. Созданный первоначально для потребностей вычислительной математики он стал активно использоваться в теории управления [11-14], исследования операций [15,16], теории игр [17,18].

   Начиная с конца 70-х годов, методы теории нечетких множеств начинают применяться в экономических исследованиях. Так, в работе  [19] рассмотрена система дифференциальных уравнений с нечеткими параметрами и введена матрица «затраты-выпуск» Леонтьева, элементами которой являются треугольными нечеткие числа. Отметим здесь же монографию [20], в которой представлен широкий спектр возможных применений теории нечетких множеств — от оценки эффективности инвестиций до кадровых решений и замен оборудования.

   Особо выделим здесь использование треугольных нечетких чисел. Укажем в этом направлении работы по проблемам инвестирования [19-24]. Теория треугольных чисел дает возможность свести качественные экспертные оценки к количественным, числовым (правда нечетким). С другой стороны, нечеткие множества представляют эксперту большую гибкость. Например, при ответе на вопрос, каким будет ожидаемый экономический показатель, эксперт может указать пессимистическую , оптимистическую  и наиболее вероятную . Полученную информацию можно объединить в виде нечеткого треугольного числа . Именно такой подход и используется в данной работе.

   Настоящая статья посвящена вопросам применения треугольных нечетких чисел к задаче определения некоторых характеристик экономических объектов. На основе нечетких оценок функции избыточного спроса представлена модификация динамической модели Вальраса рынка одного товара. Получены оценки интервального типа положения равновесия модели и условия его устойчивости. Изучена краевая задача, эквивалентная в некотором смысле обычной динамической модели Вальраса рынка одного товара с постоянными коэффициентами подстройки цены предложения, а также цены спроса.  Построено с гарантированной степенью точности приближенное решение указанной краевой задачи. Эти результаты перенесены на случай рассматриваемой модификации модели Вальраса интервального типа. Поставлена и решена задача об  — кратном изменении цены товара к конечному моменту времени.

   Нечеткая модель Вальраса. Рассмотрим модифицированную линейную модель Вальраса  [25] рынка одного товара с кусочно-постоянным запаздыванием цены предложения.

   Здесь  – функция избыточного спроса,   – функции спроса и предложения,  – цена единицы товара в момент времени  – лаг запаздывания цены,   — коэффициент скорости реакции  — положительные параметры,  – целая часть числа , числа  — коэффициенты  подстройки цены предложения,  – неконтролируемое возмущение.

   Выразим  через  и положим  . Тогда уравнение (1) примет вид:

   В (1) предполагается, что все параметры и сама функция избыточного спроса имеют точные значения. Однако на практике, как правило, точные значения получить невозможно.

   Будем считать, что параметры, входящие в уравнение (1), представляют собой треугольные числа . Число  представляет собой наименьшее возможное значение параметра ,  -наибольшее возможное значение , а  -наиболее вероятное значение . Функции из (1) также считаются треугольными [7], т.е. , где  имеют тот же смысл, что и .Отметим, что арифметические действия и дифференцирование над нечеткими треугольными функциями производятся по правилам, с которыми можно ознакомиться, напр., в [7].

   Пусть теперь нечеткие параметры в  таковы, что для каждой компоненты функции  можно получить аналог (2)

   Для каждого из этих равенств существует точка равновесия, в которой скорость изменения соответствующей цены равна нулю. Эти положения равновесия при  определяются равенствами [25]:  . Известно [25], что полученные положения экспоненциально устойчивы. Последний факт позволяет говорить о стабилизации цены. Равновесная цена здесь описывается треугольным нечетким числом вида . Данное треугольное число можно считать нечетким равновесием задачи (1).

   Выделим отдельно случай, когда нечеткое равновесие может стать четким числом. Эта ситуация возникает, если . Разумеется и в данной ситуации будет иметь место экспоненциальная устойчивость.

   Представим теперь описанные процессы с помощью решения некоторой краевой задачи. Рассмотрим сначала детерминированный случай.

   Краевая задача и ее решение. Возьмем некоторое n и рассмотрим (1) на промежутке времени .

   Поставим задачу об  — кратном изменении цены товара к конечному моменту времени :

   Запишем краевое условие (3) в виде

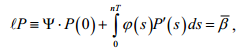
где  ([1], стр. 32).  По числу  и функции   подберем функцию  такую, что .

   Тогда система уравнений

однозначно разрешима [1] и ее решение имеет представление:

где .

   Применим «-подстановку» (4) к уравнению (2)

   Отсюда приходим к следующему  интегральному уравнению

где .

   Заменим уравнение (5) уравнением:

с вырожденным ядром , где функции  определяются по кусочно-постоянной аппроксимации ядра , соответствующей равномерному разбиению квадрата  на малые квадраты с такой стороной, чтобы выполнялось требование точности. Функции  будет соответствовать аналогичная (1), (2) краевая задача.

   Известно [2], что краевая задача (2),(3) однозначно разрешима, причем ее приближенное решение имеет представление

с точностью

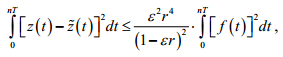
и, кроме того,

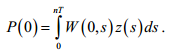
   Решение краевой задачи в нечетком случае. Выводы. Пусть задача приобретает нечеткий вид. Как и в пункте 2 настоящей статьи, будем считать нечеткие параметры такими, что аналог уравнения (2′) записывается в виде . Берем вновь некоторое натуральное число   и рассматриваем уравнения (2′) при . Задачу об  -кратном изменении цены товара к моменту времени  ставим в нечетком виде, считая и  и  треугольными числами: . Данное условие распадается на три: . Таким образом, с учетом (2′) для каждого  приходим к задачам, решенным в пункте 3 работы. Следовательно, поставленная задача однозначно разрешима и решение можно записать с помощью представления (7).

   В заключение отметим, что изучение нечеткой динамической модели Вальраса рынка одного товара с постоянными коэффициентами подстройки цены предложения показало, что при условиях на параметры модели, связанных с уравнениями (2′), можно говорить о существовании положения равновесия и его экспоненциальной устойчивости. В случае возникновения задачи об -кратном изменении цены товара к моменту времени  можно определелить для приближенного решения краевую задачу, эквивалентную в некотором смысле поставленной. Это позволяет построить с гарантированной степенью точности приближенное решение исходной краевой задачи. Указана методика определения решения задачи в нечеткой постановке.

Список литературы

1. Азбелев Н.В., Максимов В.П., Рахматуллина Л.В. Введение в теорию функционально-дифференциальных уравнений. – М.:Наука, 1973. – 384 с.
2. Максимов В.П., Румянцев А.Н. Краевые задачи и задачи импульсного управления в экономической динамике. Конструктивное исследование// Известия Вузов. Математика, 1993, №5. –С. 56-71
3. Суслов В.И. Об экономических измерениях: вероятность и достоверность, математическое моделирование, большие данные, электронная статистика// Вопросы статистики, 2016, №1(4). – С.38-46
4. Никайдо Х. Выпуклые структуры и математическая экономика. – М.: Мир, 1972. – 519 с.
5. Goodwin R.M. Dynamical coupling with especial reference to markets having production lags// «Econometrica», 1947, №15. – С.181-204
6. Аллен Р. Математическая экономия. – М.: Иностранная литература, 1963. – 670 с.
7. Калман Р., Фалб П., Арбиб М. Очерки по математической теории систем. – М.: Мир, 1971. – 400 с.
8. Zadeh L.A. Fuzzy Sets// «Inf. And Control», 1965, № 8. – С. 338-353
9. Wong C.K. Fuzzy Topology. Fuzzy Sets and their Applications to Cognitive and Decision Processes. – New York: Academic Press, 1975. – 507 p.
10. Zadeh L.A.: The concept of a linguistic variable and its application to approximate reasoning// Inf. Sci., 1975, Part I, № 8. — S. 199-249; Part II, №8. – S., 301-357; Part III, №9. – S.43-80
11. Гусев Ю.М., Ефанов В.Н., Крымский В.Г., Рутковский В.Ю. Анализ и синтез линейных интервальных динамических систем (состояние проблемы)// Известия АН. Техническая кибернетика, 1991, №1. —  С. 3-23; № 2. – С. 3-30
12. Ащепков Л.Т., Давыдов Д.В. Стабилизация наблюдаемой линейной системы управления с постоянными интервальными коэффициентами// Известия вузов. Математика, 2002, №2. – С. 11-17
13. Ащепков Л.Т., Колпакова Г.Э., Стегостенко Ю.Б. Стабилизация нестационарной линейной дискретной системы управления с интервальными коэффициентами по наблюдениям фазовых состояний//»Автоматика и телемеханика», 2002, № 5. – С. 3-11
14. Давыдов Д.В. Локальная стабилизация интервально наблюдаемой системы с неопределенными параметрами//»Вычислительные технологии», 2003, №1(8). – С. 44-51
15. Ащепков Л.Т., Косогорова И.Б. Минимизация квадратичной функции с интервальными коэффициентами// Журнал вычислительной математики и математической физики, 2002, №5(42). – С. 653-664
16. Левин В.И. Сравнение интервальных величин и оптимизация неопределенных систем//» Информационные технологии», 1998, №7. – С. 22-32
17. Ащепков Л.Т., Гуторова С.В., Карпачев А.А., Ли С. Интервальные матричные игры// Дальневосточный математический журнал, 2003, №2. – С. 276-288
18. Шашихин В.Н. Решение интервальной матричной игры в смешанных стратегиях// Известия РАН. Теория и системы управления, 2001, №5. – С. 97-104
19. Buckley J.J. The fuzzy mathematics of finance// Fuzzy Sets and Systems, 1987, Vol. 21. – S.257—273
20. Кофман А., Хил Алуха X. Введение теории нечетких множеств в управлении предприятиями. – Минск: Высш. Школа, 1992. – 224 с.
21. Kuchta, D. Fuzzy capital budgeting// «Fuzzy Setsand Systems», 2000, Vol. 111. – S. 367—385
22. Lefley, F., Sarkis, J. Applying the FAP model to the evaluation of strategic information technology projects// International Journal of Enterprise Information Systems, 2005, №1. – S. 69—90
23. Huang X. Optimal project selection with random fuzzy parameters// Int. J. Production Economics, 2007, Vol. 106. – S. 513—522
24. Недосекин А.О. Нечетко-множественный анализ риска фондовых инвестиций. – М.: Сезам, 2002. – 181 с.
25. Симонов П.М. Исследование устойчивости решений некоторых динамических моделей микро- и макроэкономики// Вестник Пермского ун-та. Математика. Информатика. Механика, 2003, №1. — С. 88-93