
УДК 330.42
DOI 10.24412/2413-046Х-2021-10030
ОЦЕНИВАНИЕ ПАРАМЕТРОВ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЭКОНОМИКО-ЭКОЛОГИЧЕСКОЙ ЗАДАЧИ МЕТОДОМ МОДУЛИРУЮЩИХ ФУНКЦИЙ
ESTIMATION OF PARAMETERS OF A MATHEMATICAL MODEL OF ECONOMIC AND ECOLOGICAL PROBLEM BY THE METHOD ОF MODULATING FUNCTIONS
Воробьева Елена Юрьевна, старший преподаватель, Пермский национальный исследовательский политехнческий университет, г. Пермь
Пепеляева Татьяна Федоровна, кандидат технических наук, доцент, Пермский национальный исследовательский политехнический университет, г. Пермь
Иванкин Валерий Юрьевич, кандидат технических наук, доцент, Пермский национальный исследовательский политехнический университет, г. Пермь
Vorobeva E.U., lena-vorobey@yandex.ru
Pepelyaeva T.F., tania4072@gmail.com
Ivankin V.U., sweet4072@gmail.com
Аннотация. В статье реализован метод численной оценки параметров математической модели загрязнения сточных вод при добыче полезных ископаемых на территории Российской Федерации. Оценка производилась по методу скользящих модулирующих функций. На основе полученных результатов сделан прогноз на следующий период времени.
Summary. The article implements the method of numerical estimation of the parameters of the mathematical model of wastewater pollution during mining in the territory of the Russian Federation. The estimation was performed using the method of sliding modulating functions. Based on the results obtained, a forecast is made for the next time period.
Ключевые слова: задача вариационного исчисления, экология, объемы загрязнения, параметры модели, метод модулирующих функций.
Keywords: the problem of calculus of variations, ecology, pollution volumes, model parameters, the method of modulating functions.
При моделировании различных экономико-экологических процессов вид математической модели может быть известен заранее. Чтобы идентифицировать известную модель и дать оценку ее параметрам, необходимо решить «обратную» задачу, используя конкретные экспериментальные данные исследуемого процесса. Такие задачи хорошо известны и играют важную роль в различных областях науки. Оценка неизвестных параметров считается задачей идентификации в узком смысле слова [1].
В предыдущих публикациях [2,3] нами была построена математическая модель (1-3) загрязнения окружающей среды на основе производственной функции Кобба-Дугласа, произведен анализ зависимости капитала и объема загрязнения от доли средств, выделяемых предприятиями на очистные сооружения, и предложены рекомендации по оптимальным вложениям средств на очистные сооружения.
Модель (1-3) загрязнения сточных вод при добыче полезных ископаемых описывает зависимость объемов потребления, капитала и загрязнения [4,5,6].
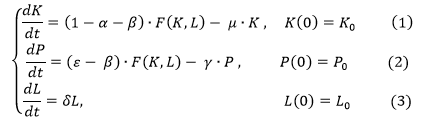
где α, β – доли выпуска, предназначенные для потребления и уменьшения загрязнения соответственно (0 ⩽ α ⩽1, 0⩽ β⩽1, α+β⩽1);
є – доля объема загрязнения от выпуска;
μ – темп амортизации;
γ – естественная убыль отходов в каждый момент времени;
δ – годовой темп прироста числа занятых в производственной деятельности;
F(K,L)=a0×Ka1×La2 – производственная функция Кобба-Дугласа; параметр a0 – коэффициент нейтрального технического процесса, a1 и a2 коэффициенты эластичности объема производства по затратам капитала и ресурса труда соответственно;
K=R(t), P=(Pt), L=L(t) – объемы капитала, загрязнения и трудовых ресурсов соответственно, зависящие от времени.
Производственная функцию Кобба-Дугласа имеет вид:
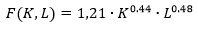
Для ее построения были использованы данные статистики загрязнения сточных вод на территории РФ при добыче полезных ископаемых за 2008-2019 гг. [2,7]. Также, с учетом статистических данных, зададим коэффициенты μ=0,16; є=0,3; γ=0,1 .
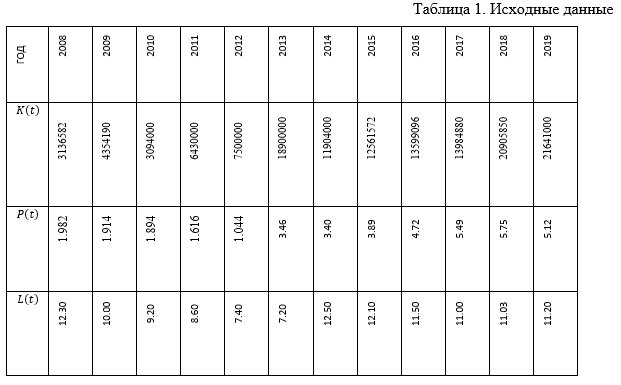
Будем предполагать, что параметры найденной производственной функции стабильны на некотором временном промежутке и характерны для данной отрасли, т. е. считаем, что на этом промежутке времени технология производства остается неизменной.
Целью настоящего исследования является оценка средних неизвестных параметров α, β долей выпуска на некотором промежутке времени [0,T], предназначенных для потребления и уменьшения загрязнения соответственно модели (1-3) и среднего δ годового темпа прироста числа занятых в производственной деятельности.
Так как модель (1-3) представляет собой систему дифференциальных уравнений, то для оценивания параметров модели удобно использовать метод скользящих модулирующих функций (м-метод). Метод подробно описан в монографии Пучкова В. Ф. и Грацинской Г. В. [8]. Он позволяет оценить средние значения коэффициентов моделей, не решая саму краевую задачу [1]. Идея м-метода состоит в следующем: задается некоторая непрерывно-дифференцируемая на функция , равная нулю на концах отрезка φ(0)= φ(T)=0, на которую умножается дифференциальное уравнение. Будем называть ее «скользящей модулирующей функцией» [1,8,9]. Дифференцирование решения «переносится» на дифференцирование заданной функции, которую можно выбирать с достаточной степенью гладкости. В итоге исходное дифференциальное уравнение заменяется аналогичным ему интегральным уравнением.
В качестве модулирующей выберем функцию вида φ(t)=sin wt, где wt=π. Данная функция непрерывно-дифференцируема на интервале от [0,T] и равна нулю на концах исследуемого интервала времени [7].
Среднюю оценку параметра β найдем из уравнения (2):
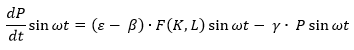
Интегрируя его по отрезку [0,T], получаем:
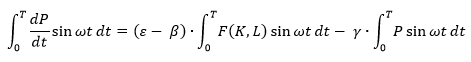
Используя формулу интегрирования по частям и учитывая нулевые значения на концах отрезка, получим:
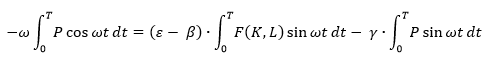
Окончательно c учетом F(K,L)=a0×Ka1×La2:
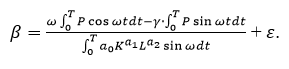
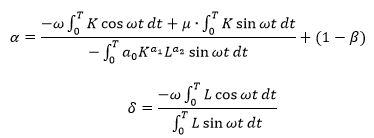
Значения определённых интегралов были рассчитаны путём численного интегрирования, получили следующие средние оценки: β=0,299, α=0,605, δ=0,299.
По результатам исследования можно сделать вывод о том, что предприятиями по добыче полезных ископаемых около 60% от выпуска продукции отчисляется на потребление, 29% на уменьшение загрязнения и 5% на годовой прирост числа занятых в производственной деятельности.
Учитывая полученные данные параметров, построим модель (1-3):
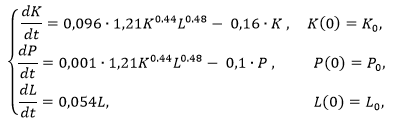
характеризующую данный вид производства. Использовать же результаты возможно, например, составляя прогноз состояния системы на следующий промежуток времени.
Решая задачу (1-3), получили, что в следующем расчетном году объем капитала должен составлять 18179098 тыс. руб., численность работников 11,76 тыс. человек, объем загрязнения сточных вод 6 тыс. тонн.
Итак, в работе была проиллюстрирована эффективность метода модулирующих функций для решения обратных задач – были произведены оценки параметров данной модели м-методом. Это дало возможность от операции дифференцирования табличной функции сделать переход к допустимой для нее операции интегрирования.
Т. к. все преобразования, которые производились в м-методе, эквивалентны исходному уравнению, то можно утверждать, что погрешности м-метод теоретически не имеет [1]. Практически источником погрешностей может являться численное вычисление интегралов, минимизировать которые можно при использовании современных вычислительных систем.
Список литературы
- Шумафов М.М., Цей Р.: Метод модулирующих функций и его применение при решении обратных задач.
- Математическая модель загрязнения окружающей среды с производственной функцией./ Е. Ю. Воробьева, Агаркова Н. И. // Наука и бизнес: Пути развития. Математические и инструментальные методы в экономике. Москва. — 2016 .— № 7 (61) .— С. 53-59.
- Вариационный метод решения задачи экономико-экологического моделирования/ Е. Ю. Воробьева, Т. Ф. Пепеляева, В. Ю. Иванкин // Наука сегодня: история и современность: материалы междунар. научн.-практ. конф., [г. Вологда], 31 окт. 2018 г. В 2 ч. ч. 2./ Научн. центр Диспут. – Вологда: Маркет, 2018. – С. 17-18.
- Красс М.С., Чупрынов Б.П. Математические методы и модели для магистрантов в экономике //Учебное пособие.-СПб.:Питер, 2006-496с.:ИЛ.
- Гринева Н.В. Экономико-математическое моделирование: математическое моделирование микроэкономических процессов и систем: Учебное пособие. М.: Финакадемия, 2008. 104 с.
- Гринин А.С., Орехов Н.А., Новиков В.Н. Математическое моделирование в экологии: Учеб.пособие для вузов. – М.: ЮНИТИ-ДАНА, 2003. – 269с. – (Серия «Oikos»).
- Российский статистический ежегодник [Электронный ресурс]: Федеральная служба государственной статистики: Москва, 2008-2019 г. URLhttp://www.gks.ru
- Пучков В.Ф. Математические модели макроэкономики: Учебное
пособие. – 3-е изд. перераб. и доп. – Гатчина: Изд-во ГИЭФПТ, 2010. – 199 с. - Пучков В.Ф., Грацинская Г.В., Методология построения математических моделей и оценка параметров динамики экономических систем: монография. – Москва: Креативная экономика, 2011.– 240 с.


