
DOI 10.24411/2413-046Х-2020-10631
Innovation strategies in health economics: a force that makes blood move and game of gravity in it – futuristic economic plans
Soham Samajpaty, Department of General Medicine; International Faculty, Russian National Research Medical University named after N.I. Pirogov, sohamsamajpaty@gmail.com
Samrat Ray, PHD Scholar, Economics, the Institute of Industrial Management, Economics and Trade, Peter the Great Saint Petersburg Polytechnic University Russia, samratray@rocketmail.com
Summary. For centuries, there persists unsolved mystery of human physiology and rheumatology. It is still unclear how venous return of blood inside human veins happen and how being in gravitational field, our blood flow is affected by gravitational force. Theories have been put up but with discrepancies and fallacies. A deep mathematical study and dynamical derivations have been carried on to show how gravitation influences blood flow and what exactly is the shear equation of the blood. Equation has also been derived for calculating blood pressure of any blood vessel at a particular moment.Based on the mathematical findings have come up with futuristic economical plan and technology development scheme to enhance and apply the theory in practical clinical application around the globe. We are in a world which might in upcoming 5000-6000 years succumb to increasing solar energy. As per Dr. Meghnad Shah’s conclusion about photonization of Helium, humans won’t be able to uphold in this planet for long. Our work provides the far future outlook about extra-terrestrial human settlement as well. World has to take up our findings with utmost importance and rapidly work towards realization of such mammoth dream.
Keywords: Hemodynamics, Health Economics, Space-medicine, Space-health fimance
Introduction
Extensive work on hemodynamic and blood movement and its nature has been conducted and theories have been put forward. The already existing theory states skeletal muscle contraction as a factor for venous return but our ambition is to mathematically find out how acceleration due to gravity and force of gravity affects the flow of blood. We would also try to investigate the shear which makes blood as a continuum to move. If we take up a clinical case where the subject has paralysis and skeletal muscles are not contracting, we fail to explain how blood is returning. If considerable amount of blood fails to return it means that it is antagonistic to Fick’s principle. Considering the fluid mechanics, it is obvious that since blood is a continuum, it has to have a shear for movement. Shear here are the unbalanced force components which make fluid movement possible. In 1895 Leonard Hill from University College, London, Department of Physiology made a detailed study on effect of gravitation on blood and cerebrospinal fluid in his paper “THE INFLUENCE OF THE FORCE OF GRAVITY ON THE CIRCULATION OF THE BLOOD”. But he failed to provide mathematical explanations to the phenomenon he investigated.
This simple principle can be well grounded and applied in health economics for production ethics in vaccination and medicinal recovery process. According to Austrian school of economics, liberal guidance in ethics as well as CSR drives the foundation for development of health related recovery which can be fastened if the theoretical foundations of classical economics can be suppressed. Hayek further argues on the need for retrospective knowledge based on logic and deductive theory rather than induction in various journals. The need for CSR and ethics in the production campaign of haemodynamical solution to recovery analysis can be far outreached and sustained.
Jason H Hamann, Zoran Valic, John B Buckwalter and Philip S Clifford of Medical College of Wisconsin and Veterans Affairs Medical Center, Milwaukee, Wisconsin, in their paper titled ‘Muscle pump does not enhance blood flow in exercising skeletal muscle”; 2002 made several experiments on hind-limb blood flow in Mongrel dog. They too concluded that venous blood from cutanoeus branches maybe affected by skeletal muscle contraction but venous return as a whole cannot be affected by it. Although they suspected that unsynchronized muscle contraction may help venous return to sudden extent during exercises. This is because during exercise or any kind of physical activity like walking, jogging, etc. the suction-impulse pumps (SIP) and muscle-venous-articular pumps (MVAP) are stimulated (Comparison of reduction of edema after rest and after muscle exercises in treatment of chronic venous insufficiency; Belczak Cleusa Ema Quilici, Cavalheri Gildo, Jr, Jose Maria Pereira de Godoy, corresponding author- Belczak Sergio Quilici, and Caffaro Roberto Augusto)
The authors effectively kept their points because synchronized skeletal muscle contraction means two force vectors acting towards each other; resulting into zero movement of fluid in between by nullifying each other. But unsynchronized skeletal muscle contraction will give rise to unbalanced force vectors which might help the fluid in movement.
Therefore, it is obvious that skeletal muscle contraction is a minor factor to influence the movement. In this regard, effect of gravitation has to be studied and understood as well gravitation.
The aim of the study was to investigate an explanation for such phenomenon of return of blood to heart without contraction of skeletal muscle and effect of force of gravity in this regard.
Methods
For centuries, there persists unsolved mystery of human physiology and rheumatology. It is still unclear how venous return of blood inside human veins happen and how being in gravitational field, our blood flow is affected by gravitational force. Theories have been put up but with discrepancies and fallacies. A deep mathematical study and dynamical derivations have been carried on to show how gravitation influences blood flow and what exactly is the shear equation of the blood. Equation has also been derived for calculating blood pressure of any blood vessel at a particular moment. Based on the mathematical findings have come up with futuristic economical plan and technology development scheme to enhance and apply the theory in practical clinical application around the globe. Our work provides the far future outlook about extra-terrestrial human settlement as well. Futuristic economic scheme have been proposed based on the equations.
We took
- The principles of hemodynamic as a fundamental instrument of investigation.
- Calculus was used as a mathematical tool.
- Study of blood’s surface tension and thus its nature of flow was investigated.
- General mechanics to clarify blood movement through bended blood vessels.
As per law given by George Simon Ohm for electrical circuits (tr., The Galvanic Circuit Investigated Mathematically) (1827)
dV = I x R; where we calculate V = potential difference
I = current passing through the conductor and
R = resistance
In hemodynamics same analogical relationship is used to derive the relationship between pressure, rate of flow and resistance of vessel.
dP = Q x R; where dP = pressure difference
Q = flow of blood through vessel
R = resistance of vessel
But force exerted by blood on blood vessel in not being calculated here. By using relationships of general mechanics, we may come to few conclusions. Although above relationship does successfully describes the resistance factor.
We know,
P = F/A (where, P = pressure, F = force & A = area)
We, will consider area of a cylinder since blood vessels are almost cylindrical in shape and not area of a circle.
Thus; P = F / (2πr Sf + 2πr2)
= F / 2πr (Sf +r) …………… equation (1)
Hence, from equation (1) we get that;
At constant Force; P ∞ 1 / r (Sf + r)
Pressure in small vessels > Pressure in big vessels
Here it is to be noted that the pressure maintained has to be considered as per the radius change. (Central blood pressure: current evidence and clinical importance; Carmel M. McEniery, John R. Cockcroft, Mary J. Roman, Stanley S. Franklin, and Ian B.Wilkinson)
- Maiti (Department of applied mathematics IIT BHU, India) and J. C Mishra (Institute of Technical Education & Research, Siksha ’O’ Anusandhan University, Bhubaneswar, India) describes that radius of blood vessel is not constant for a single vessel but doesn’t describes the relation between pressure and changing radius. This maybe concluded in the following manner;
For an infinitesimally small change in area of vessel to pressure, we will be considering infinitesimally small area, and will consider area of a circle as area of vessel.
Hence
P = F / A …… equation (2) (where A = area is a vector)
Or, P = F / πr2 (since, A is area of circle)
Integrating both sides as a function of radius “r” we get –
Pꭍ dr = F / πꭍ (1/ r2) dr
Or, P (r) = – F / (πr) + C (where, C = integration constant) …….. Equation (3)
At unit force applied on unit radius, when F = 1, r = 1, then P = (1/π) from equation (2).
Taking mod function in equation (3) i.e Pressure in dA area, we get C = 0
Therefore, P = – (F / πr2) ………. Equation (4)
We would consider -F = F4 for convenience of further calculations.
Negative sign in equation (4) suggests that every fluid has negative force acting against increasing or decreasing pressure gradient to prevent the change of state of motion of fluid molecules, i.e. analogous to a force providing inertia.
Here it is important to note that F4 acts in a direction opposite to the direction of increasing Pressure and Pressure will increase with shortening radius.
The equation (4) can be proven in another analogical fashion. It is as follows ;-
If we take two points with pressure and radius (P1, r1) and (P2, r2) where (P1 > P2) and (r1 > r2) then taking;-
P = F / (πr2)
Finding difference between two points;
(P2 – P1) = (F/π) (1/r22 – 1/r12)
Or, dP = (F/π) [ (r2 – r1) (r2+r1) / (r22)(r12)]
Or, dP = (F/π) (r2+r1)/(r22)(r12) dr
Integrating both sides of the above equation we get;-
ꭍ dP = (F/π) [ꭍ (r1)/(r22r12) dr + ꭍ (r2)/(r22r12) dr] ……. Equation (i)
Let us consider; (r1)/(r22r12) = i1 and (r2)/(r22r12) = i2 ; using integral function by parts with the principle; ꭍuv dx = u ꭍv dx – ꭍ[du/dx ꭍ v dx] dx; we get ;-
i1 = ꭍ r2-2r1-1 dr = (r2-2) ꭍ r1-1 dr – ꭍ [d(r2-2)/dr ꭍ (r1-1) dr] dr = r2-2 ln r1 – ꭍ[(-2r2-3) ln r1] dr = (ln r1)/r22 + 2 ꭍ(r2-3 ) (ln r1) dr … equation (ii)
Now let us consider ꭍ(r2-3 ) (ln r1) dr = i3’
I3’ = ln r1 ꭍ r2-3 dr – ꭍ [d(ln r1)/dr ꭍ r2-3 dr] dr = ln r1 (r2-2)/(-2) – ꭍ (r2-2/-2r1)dr = – ln r1/(2r22) + ½ ꭍ (1/r1r22)dr = – ln r1/(2r22) +1/2 ꭍ(r1-1)(r2-2)dr = – ln r1 (2r22) + ½ (i1) ……. Equation (iii)
So, if we consider ln r1/r22 = α and ln r2/r12 = β
Hence
i3’ = – α/2 + i1/2 ……. Equation (iv)
Similarly it can be stated; i2 = ln r2/(r12) + 2 ꭍ( r1-3) (ln r2) dr
Considering; ꭍ( r1-3) (ln r2) dr = i4’
If we consider; [ꭍ (r1)/(r22r12) dr + ꭍ (r2)/(r22r12) dr] = i
Then
i = i1 + i2 = [α + 2(-α + i1/2)] + [β +2 (-β + i2/2)] = (α – 2α + i1) + (β -2β + i2) = – α + i1 – β + i2 = – [ (α+β) – (i1 + i2)] = – Ϛ
Where Ϛ signifies integral continuity of radius.
Thus, by equation (i)
P = (F/π) [ – {(α+β) – (i1 + i2)} ] = – (F/π) Ϛ
The type of flow of blood and its rheological property is described by Reynold’s equation. But a change in the equation maybe done and reframed as –
Re = ϱ d v / η (where; Re = Reynold’s number, ϱ = density, d = diameter of vessel, v = velocity of blood flow &η = viscosity of blood)
From equation (1) and from relation [P = (ϱ Sf g)] we get;-
Re = (P 2r v) / Sf g η
Or, Re = F 2r v / 2πr (Sf + r) Sf g η
Or, Re = F v / π Sf g η (Sf + r) …………… Equation (5)
When, length of vessel and radius of vessel are constant i.e.
[π Sf g (Sf + r)] = Ж; constant.
Thus; Re = F.v /Ж η (F and v both are vector quantities)
Hence
Re = |F||v| cosϴ / Ж η ………. Equation (5)
It is to be noted that in Non-Newtonian fluids like blood viscosity; η is variable and in Newtonian fluid it is constant.
Here it can be noted that Human beings cannot be settled on planets like Mars (gmars = gearth / 2.5 approximately) or satellites like Moon (gmoon = gearth / 6 approximately). It also indicates another reason for not development of any higher life-forms in any other celestial bodies apart from Earth. It signifies that in such places the flow of blood will become highly turbulent which will lead to production of Eddy currents in blood and rupture vessel wall; leading to death.
We also know that;
F = G (Mm/R2)
[Where; F = force of gravity, G = gravitation constant, M = mass of planet, m = mass of subjected body and R = radius of the celestial body; none of which are changeable]
For two parallel flat areas of fluid of the same size A which are separated by a distance dx (Fig. 1). If the plates are moving in the same direction at different velocities V1 and V2, then the force required to maintain the speed is proportional to the difference in speed through the liquid, or the velocity gradient
F/A = η dy/dx ; where η is the viscosity of the fluid.
The shear rate describes the shearing which the liquid experiences. In other words, the velocity gradient, dy/dx, which is a measure of the change in speed at which the intermediate layers move with respect to each other is called the shear rate (γ) and its unit of measure, is the reciprocal second (s-1).
The term F/A indicates the force per unit area and is the shearing action or shear stress (τ). The unit of measurement of shear stress is dynes per square centimeter (dynes/cm2) or Newton per square meter (N/m2). According to the above statement, viscosity can be defined as shear stress over shear rate:
η = τ /γ (Where τ = V/A and γ = F/A)
We clearly may conclude that F4 acts on the opposite direction of increasing pressure gradient.

Hence, here force; considering radius of blood vessel is decreasing away from the heart; F4 will always act towards the heart.
Property of blood as a fluid
We know that after Rouleaux formation blood effectively show diffraction of light.
From this we conclude that blood is not just a viscous fluid but a multiphasic non – Newtonian multiphasic fluid with different kinds of particles immersed in it (e.g. hematorcrits, salt, variety of protein molecules, e.t.c.), where from center of unit cross-sectional area of blood is leukocyte, erythrocyte, thrombocytes and plasma respectively, towards periphery of the blood vessel. Proteins in blood act as surfactant that allows blood to resist change by external forces and keep low surface tension.
Since blood is an emulsion from the above argument, we may confer that every cell in blood has viscous drag acting on it. This force would acts as main Shear component for movement of blood continuum. But the force F4 is important in the regard how it balances or adds up to the force of gravity (f = mg).
For convenience of calculation, let us consider a neuotrophil (as it is almost a sphere). Force acting on unit area of vessel by unit area of blood
ꞙ = (fd+fd+ ….. + fdn) + [(F4+mg)] = [(nfd)+F4+mg] …….. Equation (6)
Here fd = 6πrhηv
( rh – radius of hematocrit
η – viscosity
rv – radius of vessel)
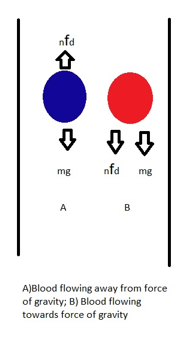
The direction of action of F4 is always towards the heart, considering narrowing blood vessels away from heart.
While putting forward this “latent shear force” as ꞙ; we might opine that blood vessels need a particular tension on walls for maintenance of the force and pressure gradient. This is supplied by the smooth muscle contraction but the action is localized. L-type calcium channels and T-type calcium channels contribute to this action (Signaling in Muscle Contraction; Ivana Y. Kuo and Barbara E. Ehrlich).
Now we can write the Pressure and force condensed equations as –
PB = ꞙ / 2πrv (Sf +rv)
When calculated for pressure in Brachial artery of radius of 4.25cm, viscosity of 3cm/g and velocity of blood 80 cm/s, then the value for pressure came as (35.57 x 105) mm Hg using equation (2) and equation (5). From this value we may conclude that for all vessels;-
PB = (P/± 5).105 [where; (P/ ± 5) = pressure reading on barometer]
(value of F4 maybe neglected in calculation as nfd is large enough for movement but F4 has the function of balancing the force of gravity.)
Similar was observed for Jugular Vein and Jugular venous pressure was found to be approximately (12.57×105) mm Hg. But it is to be noted here that we cannot assert a mathematical formula here. But can just say that Pbarometric in the expression asserts the approximate pressure on the particular blood vessel, neglecting the correction factor.
The correction factor here is due to the fact that we are here calculating the net pressure on the whole blood vessel of unchanged radius and not force exerted on a small cross sectional area. Hence, net pressure logically will be manifold, much more compared to that on a cross-sectional area. Neglecting the correction factor, we may get an idea of all the blood vessels in human body. This may find application in surgical procedures of blood vessels, transplantation and others. For all blood vessels, “fd” will be equal. But while in practice, a patient’s blood hematocrit value has to be calculated to find out the factor “n”.
It is found that changes occur in flow of blood in supine position from seated or standing posture (“Cardio-respiratory effect of change of body position”; Thomas J Coonan and Charles E. Hope). In Thomas’ and Charles’ “Cardio-respiratory effect of change of body position” it has been stated that in erect position cardiac output decreases about 20-40% and stroke volume decreases as well 40-50% but mean arterial pressure remains almost constant but may increase up to 18%. Cerebral blood flow on the other hand decreases 20%. But in the paper proper mathematical logic has not been put forward to explain the phenomenon.
In erect posture: force of gravity (mg) and F4 balances each other when blood is flowing towards the heart and nfd efficiently gives the force for movement without any resistance.
When it comes to cerebral blood flow things are reversed; now vein (jugular vein) is carrying blood towards gravity and arteries (carotid artery, basilar artery, etc) are carrying blood against the gravity and hence the 20% decrement. F4 is additive with Mg. It is obvious that the body will try to adapt to changes in order to maintain the principle of Guyton’s argument that states – cardiac output is dependent on venous return and that the heart can only pump what has been returned to it. In this attempt, cardiac output and stroke volumes undergoes an 18% increment.
In supine posture: In supine position as such no change is noticed. This is very obvious because in supine position force of gravity (mg) acts vertically down whereas nfd and F4 works in the manner which they are expected to work. The force of gravity (mg) is neutralized by normal reaction force given by the surface in opposite direction, hardly affecting the fluid flow.
In a classic case, described by Piorry in Arch Gen. de Med. 1826 a patient was encountered by him with low pulse rate, rare and strenuous respiration, weak and irregular heart beat and pale face. The patient had been supported by his friend in sitting posture. He had been trampled upon the belly by horse. Piorry laid the patient down horizontally and immediately his eyes opened and he recovered very fast. But after Piorry’s departure, the patient was taken back and made to sit in his carriage. On doing so he immediately lost consciousness and died.
Such case has the same explanation as has been described above to explain the phenomenon from Thomas’ and Charles’ “Cardio-respiratory effect of change of body position”
Meniscus of blood
It is being said that blood has a laminar convex meniscus. But –
We know,
Surface tension of Mercury is 425 x 10-3 Nm-1
Surface tension of Water is 75 x 10-3 Nm-1
Surface tension of Blood is (~55.8 x 10-3) Nm-1 [E. Encir & J. Rosina]
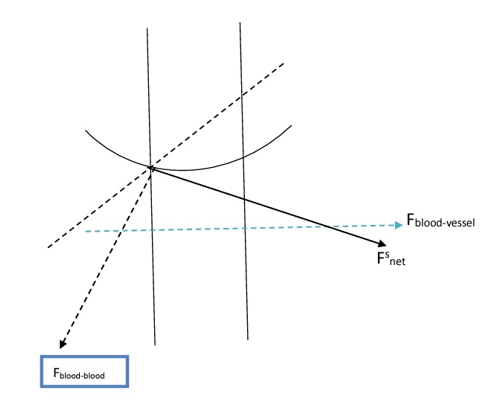
Hence, we see that surface tension of blood is lower even that water. Hence adhesive force here is greater than cohesive force and net force will act towards the force between blood and vessel and not towards that of blood to blood. Hence we may conclude that blood will have a concave meniscus and not a convex meniscus.
As shown in the figure, let us consider blood in a blood vessel. We resolve the surface tension force into force between blood-vessel and blood-blood (Fblood-vessel and Fblood-blood). The Fnet vector will act towards Fblood-vessel as surface tension is low and the surface tension being low, the cohesive force in also very low. Hence, vessel will attract blood fluid particles more than blood fluid itself. Hence for obvious reason, the angle of contact is more than acute angle i.e. (Өc >900). Hence, blood doesn’t well the vessels.
Mechanism of blood fluid movement through bended blood vessel
To understand what forces are acting on unit volume of blood moving through a bended blood vessel we should recall analogy to water moving through a bended pipe.
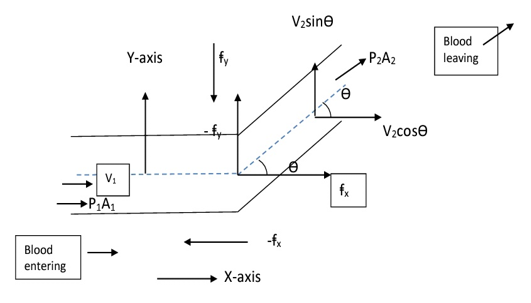
Hence on X-axis;-
P1A1 – P2A2cosӨ – ꞙx = ϱQ(V2cosӨ – V1)
Thus, ꞙx = P1A1 – P2A2cosӨ + ϱQ (V1 – V2cosӨ
And, on Y – axis
0 – P2A2sinӨ – ꞙy = ϱQ (V2sinӨ – 0)
Thus, ꞙy = – P2A2sinӨ – ϱQ V2sinӨ
Therefore
fnet = √(ꞙx2 + ꞙy2) tanӨ = (ꞙy / ꞙx)
Ө = tan-1 (ꞙy / ꞙx)
Results
The postulates here has been created to uphold economic indicators which foresee a possible development of medication studying the dynamics of blood and its physical orientation which can be applied with proper CSR to lead the human civilization to future and make extra-terrestrial human settlement possible. Apart from that the formula PB = ꞙ / 2πrv (Sf +rv) developed can be utilized for software development using programming language technology where relevant data will be put in the system and it would declare the blood pressure of the required blood vessel. A medical professional might use this opportunity to use local vasodilators before surgery and avoid any unnecessary or unwanted bleeding on incision. This technique might be used efficiently throughout the globe for efficient patient management. Equation no. 5 is revolutionary in itself and has to be utilized while considering extra-terrestrial human settlement. Space agencies will have to join hands and have to find out adequate conditions for the purpose. Moreover apart from this the paper has made justice to classical physics by redefining and proving the “shear equation” of blood.
Previously it was impossible to explain how blood is returning towards the heart against the force of gravity without contraction of skeletal muscle in subjects with paralysis. But now we understand how this phenomenon can be explained. Although attempts were made previously but without any concrete conclusion. Apart from this we know how acceleration due to gravity is influencing the movement of blood from the relation; Re = |F||v| cosϴ / Ж η. Hence, “Latent Shear Postulate of blood” is being put forward. We can now say that this latent shear is responsible for movement of “blood continuum”. Cases studied by Piorry and in Thomas’ and Charles’ “Cardio-respiratory effect of change of body position” can also be effectively explained by this postulate. We also come to conclusion that human settlement in other planets or satellites is next to impossible and also found the reason for not development of higher life-forms on other planets.
Discussion
- From the equation; PB = ꞙ / 2πrv (Sf +rv) we find the relation between pressure and force in a blood vessel given by blood. Here we can measure the “distance travelled by blood” (Sf) as the distance of the point on the vessel from heart (aorta in case of artery / right atrium in case of veins). We don’t need to think about direction as displacement of blood is always zero. This equation also gives the reason for venous return.
- From the relation; Re = |F||v| cosϴ / Ж η [where Ж = π Sf g (Sf + r)] we find the effect of force of gravity on blood flow. From here we may resolve the reason for cardiovascular diseases in low (or zero) gravity. We conclude from here that human settlement in other planets or satellites are not possible as the flow of blood will become turbulent, producing eddy currents, Korotoff’s sound, tachycardia and cardio-vascular collapse, respectively.
- We also conclude that blood cannot have a convex meniscus but will have a concave meniscus because of low surface tension.
- From the relation; P = – (F / πr2) ; we get relation which indicates the “inertial anti-pressure gradient drag” of blood.
- From the relation; ꞙ = [(nfd)+F4+mg] we find force (or latent shear) exerted by unit area of blood on unit area of blood vessel.
- Although mathematically postulated but technical limitations are present. Because of which it’s not possible to properly calculate all the postulated equations. Further research is needed in this regard and at present time due to lack of technological instrumentation many mathematical reasoning stated above can’t be verified and thus dependence on theoretical knowledge is only probable way.
It is imperative to say that medication is the foremost integral part of health economics and its ethical usage and structure propounds to human benefit and economic developments.
Bibliography
- “Muscle pump does not enhance blood flow in exercising skeletal muscle”; JASON J. HAMANN, ZORAN VALIC, JOHN B. BUCKWALTER, AND PHILIP S. CLIFFORD Medical College of Wisconsin and Veterans Affairs Medical Center, Milwaukee, Wisconsin; 14th August, 2002
- Comparison of reduction of edema after rest and after muscle exercises in treatment of chronic venous insufficiency; Belczak Cleusa Ema Quilici, Cavalheri Gildo, Jr, Jose Maria Pereira de Godoy, corresponding author- Belczak Sergio Quilici, and Caffaro Roberto Augusto)
- “THE INFLUENCE OF THE FORCE OF GRAVITY ON THE CIRCULATION OF THE BLOOD”; Leonard Hill, 1895, University College London, Department of Physiology
- Geroge Simon Ohm ;The Galvanic Circuit Investigated Mathematically (1827)
- Central blood pressure: current evidence and clinical importance; Carmel M. McEniery, John R. Cockcroft, Mary J. Roman, Stanley S. Franklin, and Ian B.Wilkinson
- Maiti (Department of applied mathematics IIT BHU, India) and J. C Mishra (Institute of Technical Education & Research, Siksha ’O’ Anusandhan University, Bhubaneswar, India)
- On the Origin of Gravity and the Laws of Newton; Erik Verlinde, University of Amsterdam; Journal of High Energy Physics 2011
- Brookfield Engineering Labs Inc. (2010a)E. Encir & J. Rosina
- (Signaling in Muscle Contraction; Ivana Y. Kuo and Barbara E. Ehrlich).
- Guyton AC. Editors’ note. Circ Res 44: 746–747, 1979
- “Cardio-respiratory effect of change of body position”; Thomas J Coonan and Charles E. Hope


