
УДК 004.032.26
DOI 10.24411/2413-046Х-2019-19012
ИСПОЛЬЗОВАНИЕ МЕТОДА НЕЙРОННЫХ СЕТЕЙ ХОПФИЛДА ДЛЯ РЕШЕНИЯ ЗАДАЧИ МАРШРУТИЗАЦИИ В СЕТИ
Кононов А.А., институт КБСП, РТУ МИРЭА, Россия, г. Москва
Аннотация: В современных компьютерных сетях большую роль играют системы маршрутизации. Плохо организованная работа маршрутизатора приводит к снижению производительности сети и возникновению сбоев. В этой связи при проектировании сетей к ним предъявляются строгие требования по обеспечению стабильной работы и должного качества обслуживания сетевого трафика. Можно выделить широкий круг алгоритмов маршрутизации в сети. Как правило, в их основе лежат методы дискретной математики. Однако в последнее время распространение получили алгоритмы, использующие методы интеллектуального анализа данных. Так, среди них можно выделить нейросетевые алгоритмы маршрутизации. Использование нейросетей как метода непараметрической оценки может придать интеллектуальный характер процессам сетевой маршрутизации. В этой связи для решения задачи маршрутизации предложено применение сетей Хопфилда. Их во многом уникальные свойства позволяют описать процесс маршрутизации в сети в терминах нейродинамики. Это позволяет свести традиционно комбинаторные задачи к задачам нелинейной оптимизации. Последнее обстоятельство позволяет существенно ускорить их решение.
В статье предлагается решение задачи маршрутизации в сети с применением метода нейронной сети Хопфилда.
Summary: In modern computer networks, routing systems play an important role. Poorly organized operation of the router leads to a decrease in network performance and the occurrence of failures. In this regard, when designing networks, they are subject to strict requirements for ensuring stable operation and proper quality service of network traffic. You can select a wide range of routing algorithms in the network. As a rule, they are based on the methods of discrete mathematics. However, recently algorithms using data mining methods have become popular. So, among them are neural network routing algorithms. The use of neural networks as a non-parametric estimation method can add intellectual character to network routing processes. In this regard, the use of Hopfield networks has been proposed to solve the routing problem. Their many unique properties allow us to describe the process of routing in the network in terms of neurodynamics. This allows traditionally combinatorial problems to be reduced to nonlinear optimization problems. The latter circumstance can significantly speed up their decision.
The article proposes a solution to the problem of routing in the network using the Hopfield neural network method.
Ключевые слова: алгоритмы маршрутизации, нейросетевой метод, оптимизация маршрута транспортировки данных.
Keywords: routing algorithms, neural network method, data transport route optimization.
Нейронная сеть Хопфилда — полносвязная нейронная сеть с симметричной матрицей связей. Структурная схема сети Хопфилда приведена на рисунке 1.
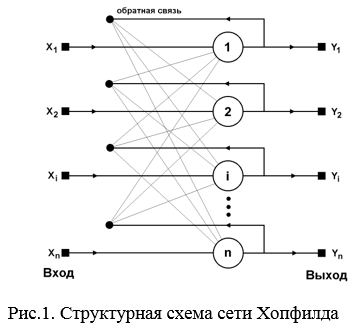
В отличие от многих нейронных сетей, функционирующих до получения ответа через определённое количество тактов, сети Хопфилда функционируют до достижения равновесия, когда следующее состояние сети в точности равно предыдущему: начальное состояние является входным образом, а при равновесии получают выходной образ.
В процессе работы динамика таких сетей сходится к одному из положений равновесия. Эти положения равновесия являются локальными минимумами функционала, называемого энергией сети (в простейшем случае — локальными минимумами отрицательно определённой квадратичной формы на n-мерном кубе). Сеть может быть использована как автоассоциативная память, как фильтр, а также для решения некоторых задач оптимизации.
Рассмотрим применение сетей Хопфилда в решении задач оптимизации. Этому способствует важное, помимо ассоциативности, свойство ее архитектуры. Оно состоит в том, что функция Ляпунова уменьшается в процессе ее функционирования. В этом отношении нейросеть Хопфилда можно интерпретировать как некоторый алгоритм оптимизации. Целевая функция может рассматриваться как энергия сети.
Число возможных целевых функций, подлежащих нейросетевой оптимизации, может быть довольно велико. Это могут быть билинейные или квадратичные функции. Сети Хопфилда могут иметь широкое применение еще и потому, что в оптимизационной постановке может быть представлен большой диапазон математических задач. К ним стоит отнести задачи линейной алгебры и дифференциальных уравнений, а также системы нелинейных уравнений.
Круг алгоритмов, формализующих маршрутизацию в сетях, достаточно широк. К одной из них можно отнести задачу коммивояжера. Она сводится к тому, чтобы обойти некоторый взвешенный граф таким образом, чтобы однократно посетить каждую его вершину. При этом необходимо выбрать путь, который обладает минимально возможной длиной. В терминах компьютерных сетей необходимо выбрать маршрут следования пакета, который при данной конфигурации проходит через каждый из ее узлов по одному разу.
Задача коммивояжера является NP-полной задачей. Для ее решения существует большое число методов решения. Компромиссное приближение можно найти с применением нейросети Хопфилда.
Целевая функция E(S) задачи поиска оптимального маршрута. Она будет включать 4 слагаемых:

Первые три слагаемых отвечают за допустимость маршрута: каждый город должен быть посещен не более чем один раз (в каждой строке матрицы имеется не более одной единицы), под каждым номером должно посещаться не более одного города (в каждом столбце — не более одной единицы) и, кроме того, общее число посещений равно числу городов N (в матрице всего имеется ровно N единиц).
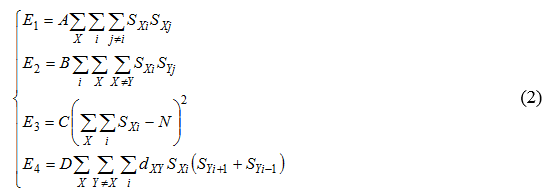
где dXY– вес ребер между узлами X и Y;
SXi– метка узла графа, приобретающая значение 0 или 1.
A, B, C, D – относительные веса слагаемых. Как правило, они задаются достаточно большими. Как показывает практика, в этом случае оптимизация является эффективной.
К меткам можно сформулировать следующие требования:
- В каждой строке маршрутной таблицы может быть только одна метка;
- В каждом столбце маршрутной таблицы может быть только одна метка;
- Число меток должно быть равно числу вершин n;
- Суммарная длина маршрута должна быть минимальной.
Метка SXi связана с потенциалом узла uXi следующим образом:

Текущее представление впоследствии можно бинаризировать, вводя пороговую оценку. При ее превышении значение метки принимается равным единице.
Начальное значение потенциала имеет вид

Входной потенциал имеет следующий вид

Модель нейродинамики работы сети имеет вид

где
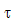
– числовой параметр.
Параметр
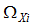
может быть выражен следующим образом:
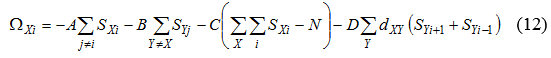
Пересчитанные в (5), (6) значения потенциала можно использовать при перерасчете меток SXi по формуле (3). Процесс повторяется некоторое число раз. Если метки обнуляют уравнения (2), выбранный вариант матрицы считается оптимальным.
Итоговую маршрутную матрицу из оценок меток SXi можно интерпретировать следующим образом. Номер столбца отвечает номеру шага обхода. Номер строки в столбце отвечает номеру узла, к которому необходимо перейти.
Традиционные алгоритмы маршрутизации носят теоретико-графовый характер и во многом ситуационный характер. Использование нейросетей как метода непараметрической оценки может придать интеллектуальный характер процессам сетевой маршрутизации. В этой связи для решения задачи маршрутизации предложено применение сетей Хопфилда. Их во многом уникальные свойства позволяют описать процесс маршрутизации в сети в терминах нейродинамики. Это позволяет свести традиционно комбинаторные задачи к задачам нелинейной оптимизации. Последнее обстоятельство позволяет существенно ускорить их решение.
Список литературы
1. Каллан Р. Основные концепции нейронных сетей. : Пер. с англ. — М. : Издательский дом Вильямс, 2001. – 287 с.
2. Осовский С. Нейронные сети для обработки информации / Пер. с польского И.Д. Рудинского. — М.: Финансы и статистика, 2002. — 344 с: ил.
3. О.А. Морозов, П.Е. Овчинников, Ю.А. Сёмин, В.Р. Фидельман. Применение теоретико-информационного подхода для обучения многослойного персептрона в задаче распознавания фонем // Вестник Нижегородского университета им. Н.И. Лобачевского, 2010, № 5 (2), с. 354–357
4. Круглов В.В., Дли М.И., Голунов Р.Ю. Нечеткая логика и искусственные нейронные сети. – М.: Физматлит, 2000. – 224 с.
5. Тархов Д.А. Нейронные сети. Модели и алгоритмы. – М.: Радиотехника, 2005. – 256 с.
6. Хайкин С. Нейронные сети: полный курс, 2¬e издание.:Пер. с анrл. – М. Издательский дом «Вильямс», 2006. – 1104 с.
References
1. Callan R. Basic concepts of neural networks. — M.: Williams Publishing House, 2001. — 287 p.
2. Osovsky S. Neural networks for information processing / Per. from Polish I.D. Rudinsky. — M .: Finance and Statistics, 2002. — 344 with: Il.
3. OA Morozov, P.E. Ovchinnikov, Yu.A. Semin, V.R. Fidelman The use of information-theoretic approach for teaching multilayer perceptron in the problem of recognition of phonemes // Bulletin of Nizhny Novgorod University. N.I. Lobachevsky, 2010, № 5 (2), p. 354–357
4. Kruglov VV, Dli M.I., Golunov R.Yu. Fuzzy logic and artificial neural networks. — M .: Fizmatlit, 2000. — 224 p.
5. Tarkhov D.A. Neural networks. Models and algorithms. — M .: Radio Engineering, 2005. — 256 p.
6. Khaikin S. Neural networks: a full course, 2nd edition .– M. Williams Publishing House, 2006. — 1104 p.


