Московский экономический журнал 5/2018

УДК 519.852
DOI 10.24411/2413-046Х-2018-15102
Севодин М.А., к.ф.-м.н., доцент, Пермский национальный исследовательский политехнический университет
Старкова Е.О., бакалавр, Пермский национальный исследовательский политехнический университет
Sevodin M.A., Starkova E.O.
О ПРОИЗВОДСТВЕННОЙ ЗАДАЧЕ С ОГРАНИЧЕНИЯМИ КОНУСНОГО ТИПА
BOUT THE PRODUCTION PROBLEM WITH CONE TYPE RESTRICTIONS
Аннотация. Рассматриваются задачи оптимальной организации производствп и задачи о смесях. Показывается, что в таких задачах естественны ситуации, в которых ограничения содержат группы неравенств, задающие некоторый многогранный конус. Для решения таких задач предлагается преобразовывать задачу в задачу в пространстве новых переменных. Базисом нового пространства является набор векторов, который является системой образующих конус векторов, или выпуклая оболочка этого набора векторов вместе с нулевым вектором представляет собой данный многогранный конус. Указывается, что такой подход к поиску решения приводит к существенным упрощениям. Описывается методика поиска образующей системы векторов. В заключение приводится пример, иллюстрирующий методику, приведенную в статье.
Abstract. Production optimization problems and blending problems are considered. It is shown that with such problems, it is natural for constraints to contain inequality groups which form some polyhedral cone. The suggested solution is to convert the problem to a problem in a space of new variables. The basis of the new space is a set of vectors forming a cone, or this set’s convex hull and the null vector form the given polyhedral cone. It is shown that the considered approach leads to substantial simplifications in searching for the solution. The methods to identify the forming set of vectors are described. The suggested methodology is illustrated with an example at the end of the article.
Ключевые слова. Линейное программирование, конус, базис, ограничения конусного типа.
Keywords. Linear programming, cone, basis, cone constraints.
Введение. Многие различные экономические проблемы сводятся к экстремальным задачам, на переменные которых накладываются некоторые условия в виде равенств и неравенств [1], [2]. Если при этом показатель качества, который оптимизируется, и ограничения задаются с помощью линейных функций, то такие задачи называются задачами линейного программирования. Одной из первых проблем, решенных с помощью теории линейного программирования, является задача оптимальной организации производства [2]. Именно этой проблемой заняты прежде всего экономические теории производства, распределения, управления предприятиями.
При использовании теории линейного программирования среди многочисленных вариантов приложений выделяются случаи со специальными линейными задачами, системы ограничений которых имеют особенный вид [2]. Дело в том, что, как правило, особые характеристики позволяют разработать для анализа таких специальных задач методы, которые являются более экономичными, чем общие методы линейного программирования. Выделению таких классов задач и посвящена данная работа. Более точно, в статье рассматриваются ситуации, в которых удается выделить группы ограничений конусного типа, то есть ограничения со следующим свойством. Если некоторый вектор удовлетворяет этим ограничениям, то и любой другой вектор, сонаправленный с первым, должен также удовлетворять таким ограничениям.
Отметим, что группы ограничений конусного типа естественно появляются во многих задачах экономического характера. Приведем некоторые примеры. Прежде всего, выделим ситуации, в которых ограничения пропорций увеличения интенсивностей технологических процессов приводят к сужению производственного множества, что объясняется причинами производственного, экономического, политического характера. В этом случае набор интенсивностей как вектор принадлежит выпуклому замкнутому конусу из неотрицательного ортанта пространства. Таким образом, возникают ограничения конусного типа. Далее, классические модели равновесия предполагают возможность выбора любых неотрицательных цен на производственные ресурсы. Но в действительности это предположение не выполняется, поэтому для баланса спроса и предложения используются ограничения на производимые и потребляемые товары и соответствующие им цены. Допустимость неценового равновесия [2] доставляет большую свободу индивидуального выбора за счет меньшей эффективности системы в целом. Исследования расширяющихся экономик типа экономики Неймана [3], в которых изменение цен образует траекторию, приводят к изучению экономик с ограничениями в виде некоторых конусов[4]. Наконец, в третьих, необходимо отметить такие проблемы, как поиск решений задач кусочно-линейного программмирования [5], модели арбитражного типа [6], динамические модели Неймана, Леонтьева [7] и другие, в которых множество решений всех ограничений представляет собой конус.
В данной статье рассматриваются задачи оптимального управления предприятиями и задачи о смесях. Показывается, что в таких задачах естественны ситуации, в которых ограничения содержат группы неравенств, задающие некоторый многогранный конус. Предлагается в таких случаях редуцировать задачу в пространство новых переменных. Базисом пространства является набор векторов, выпуклая оболочка которых представляет собой данный многогранный конус. Оказывается, что на этом пути поиск решения может быть существенно упрощен. Описывается методика поиска образующей системы векторов. В заключение приводится пример, иллюстрирующий методику, приведенную в статье.
Ограничения конусного типа и постановка задачи. Будем называть условие на вектор ![]() ограничением конусного типа, если выполнятся следующее свойство: если вектор
ограничением конусного типа, если выполнятся следующее свойство: если вектор ![]() удовлетворяет некоторому условию, то и вектор
удовлетворяет некоторому условию, то и вектор ![]() удовлетворяет этому условию. Здесь
удовлетворяет этому условию. Здесь ![]() — любое положительное число.
— любое положительное число.
Ограничения конусного типа естественным образом появляются в задачах экономического характера. Приведем два примера.
Производственная задача. Предприятие производит ![]() видов изделий, используя при этом
видов изделий, используя при этом ![]() видов ресурсов. Нормы
видов ресурсов. Нормы ![]() расхода
расхода ![]() -го ресурса на изготовление
-го ресурса на изготовление ![]() -го изделия и объемы
-го изделия и объемы ![]() запасов
запасов ![]() -го ресурса,
-го ресурса, ![]() заданы. Для единицы
заданы. Для единицы ![]() -го изделия известна цена
-го изделия известна цена ![]() . Пусть ,
. Пусть , ![]() — объем производства
— объем производства ![]() -го изделия. Требуется определить план производства изделий
-го изделия. Требуется определить план производства изделий ![]() с максимальной стоимостью. Математическая модель этой задачи записывается так.
с максимальной стоимостью. Математическая модель этой задачи записывается так.

Ограничения (2) связаны с ограниченностью ресурсов и экономическим смыслом переменных. Но естественными могут быть и требования, соответствующие другим сторонам деятельности предприятия. Так, стремление к повышению производительности может привести к следующему ограничению: отношение стоимостей потраченной на производство вектора ![]() энергии к стоимости произведенной продукции ограничено некоторым числом
энергии к стоимости произведенной продукции ограничено некоторым числом ![]() Если
Если ![]() -стоимость энергии, потраченной на изготовление единицы продукции
-стоимость энергии, потраченной на изготовление единицы продукции ![]() -го вида, то такое ограничение можно записать в следующем виде.
-го вида, то такое ограничение можно записать в следующем виде.

или в виде
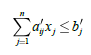
с некоторыми ![]() . Таким образом, к ограничениям (2) добавляется ограничение такого же типа с правой частью равной нулю, то есть ограничение конусного типа.
. Таким образом, к ограничениям (2) добавляется ограничение такого же типа с правой частью равной нулю, то есть ограничение конусного типа.
Приведем еще условие, связанное с исследованием рынка, на который поступает изготовленная продукция. Пусть изучение рынка показало, что продажи в стоимостном выражении некоторой группы товаров, номера которых составляют некоторое множество ![]() не превосходят некоторой доли
не превосходят некоторой доли ![]() от стоимости продаж всей продукции. Тогда опять необходимо требовать выполнения ограничения (3), причем в сумме в левой части неравенства индексы надо брать из множества
от стоимости продаж всей продукции. Тогда опять необходимо требовать выполнения ограничения (3), причем в сумме в левой части неравенства индексы надо брать из множества ![]() . Окончательно получим опять неравенство конусного типа.
. Окончательно получим опять неравенство конусного типа.
Задача о смесях. Смешивают ![]() материалов, которые различны по своим характеристикам и расходам, связанными с их получением и хранением. Меняя пропорции материалов, получают смеси различного качества и стоимости. Требуется при наименьших затратах получить смесь, которая имеет заданные характеристики. Запасы материалов при этом, как правило, считают ограниченными. Математическую модель одного из вариантов задачи о смесях можно записать так.
материалов, которые различны по своим характеристикам и расходам, связанными с их получением и хранением. Меняя пропорции материалов, получают смеси различного качества и стоимости. Требуется при наименьших затратах получить смесь, которая имеет заданные характеристики. Запасы материалов при этом, как правило, считают ограниченными. Математическую модель одного из вариантов задачи о смесях можно записать так.
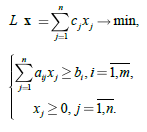
Здесь ![]() -цена единицы
-цена единицы ![]() -го материала. Считается, что каждый материал состоит из
-го материала. Считается, что каждый материал состоит из ![]() ингредиентов, причем единица
ингредиентов, причем единица ![]() -го материала содержит
-го материала содержит ![]()
![]() -го ингредиента.
-го ингредиента.
Требование, которое приводит к ограничению конусного вида, может быть здесь сформулировано так. При изготовлении смеси ![]() -й ингредиент должен содержаться в пропорции, определяемой неравенством.
-й ингредиент должен содержаться в пропорции, определяемой неравенством.
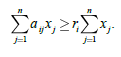
Постановка задачи и схема ее решения. Рассмотрим задачу планирования производства (1), (2). Допустим, что среди ограничений (2) имеется группа неравенств, каждое из которых имеет конусный тип. Тогда задача (2), (3) может быть записана в следующем виде.
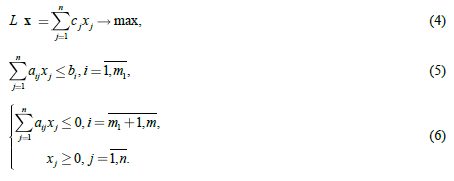
Решением группы неравенств (6) будет множество, которое представляет собой многогранный конус (предполагается, что существует ненулевое решение). Значит [3], существует такая матрица ![]() , что неравенство
, что неравенство ![]() равносильно группе неравенств (6). Здесь
равносильно группе неравенств (6). Здесь ![]() есть транспонированная строка
есть транспонированная строка ![]() .
.
Запишем задачу (4),(5), (6) в матричном виде.
![]()
где матрицы ![]() подобраны так, чтобы записанные соотношения были равносильны соотношениям (4), (5). (6).
подобраны так, чтобы записанные соотношения были равносильны соотношениям (4), (5). (6).
В [3] показано, что если взять некоторый положительный вектор соответствующей размерности, то решением системы неравенств
![]()
является многогранник ![]() . Пусть крайние точки
. Пусть крайние точки ![]() есть
есть ![]() . Тогда система этих векторов [3] такова, что конус
. Тогда система этих векторов [3] такова, что конус ![]() порождается точками .
порождается точками .
Решение поставленной задачи (1), (2) можно искать теперь следующим образом.
Осуществить переход из старой системы координат в новую систему координат, базисом которой является система векторов ![]() , образующих многогранный выпуклый конус. Тогда получится новая задача, которую можно решить симплекс-методом. Затем необходимо вернуться к старому базису, в исходную систему координат.
, образующих многогранный выпуклый конус. Тогда получится новая задача, которую можно решить симплекс-методом. Затем необходимо вернуться к старому базису, в исходную систему координат.
Следует отметить, что в новой системе координат задача будет иметь меньше ограничений, чем исходная задача. Дело в том, что требования неотрицательности новых переменных обеспечат принадлежность искомого решения нужному конусу. Отсюда следует, что процедура симплекс-метода в новой системе координат будет осуществляться проще, так как в ней будет меньше ограничений.
Рассмотрим более подробно переход от одной системы координат (СК) к другой.
Пусть ![]() — базис в старой системе координат. Выражение нового базиса через старый имеет вид линейных невырожденных преобразований базисов:
— базис в старой системе координат. Выражение нового базиса через старый имеет вид линейных невырожденных преобразований базисов:
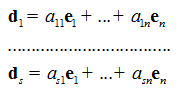
Пусть ![]() — матрица перехода от нового базиса к старому,
— матрица перехода от нового базиса к старому, ![]() ,
, ![]() — координаты некоторой точки в старой и новой системах координат, соотвественно. Тогда старые координаты будут выражаться через новые по формуле
— координаты некоторой точки в старой и новой системах координат, соотвественно. Тогда старые координаты будут выражаться через новые по формуле ![]() , а задача (1), (2) запишется в виде
, а задача (1), (2) запишется в виде
![]()
где ![]() .
.
Заметим, что для поиска крайних точек многогранника ![]() можно воспользоваться алгоритмом, предложенным в [8].
можно воспользоваться алгоритмом, предложенным в [8].
Рассмотрим пример. Фирма ежедневно производит не менее 800 кг пищевой добавки (ПД), которая состоит из смеси кукурузной, соевой и овсяной муки. Ее состав представлен в таблице 1.
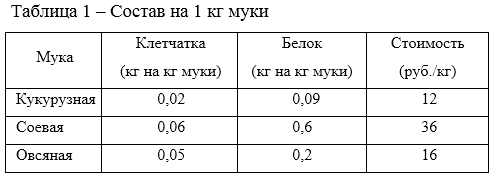
Кукурузная, соевая и овсяная мука для смеси закупается у поставщиков оптом по 12 руб./кг, 36 руб./кг и 16 руб./кг соответственно.
Диетологи требуют, чтобы в пищевой добавке было не менее 30% белка и не более 5% клетчатки. Фирма хочет определить рецептуру смеси наименьшей стоимости с учетом требований диетологов.
Составим математическую модель задачи: ![]() — количество (в кг) соответственно кукурузной, соевой и овсяной муки, используемой в производстве ПД. Тогда
— количество (в кг) соответственно кукурузной, соевой и овсяной муки, используемой в производстве ПД. Тогда
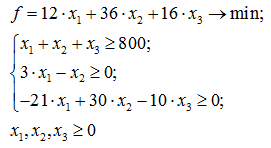
Выберем в качестве ограничений, описывающих конус, следующие неравенства: 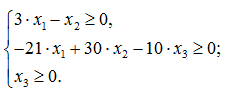
В таком случае матрица этих ограничений 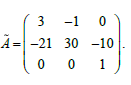
Возьмем некоторый положительный вектор ![]() и построим уравнение
и построим уравнение ![]()
Пусть ![]() , тогда
, тогда 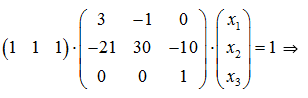
![]()
Найдем крайние точки, для этого составим систему S из найденного уравнения и трех ограничений на конус, при этом заменив знаки неравенства равенствами:
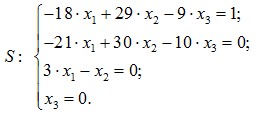
Перечислим все подсистемы из трех уравнений в ![]() (табл. 2).
(табл. 2).

Каждая из этих подсистем имеет единственное решение: A1: 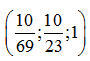 , A2:
, A2: 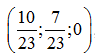 , A3:
, A3: 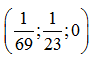 , A4:
, A4: ![]() , соответственно. Последняя точка не удовлетворяет системе S, следовательно, она не является крайней точкой.
, соответственно. Последняя точка не удовлетворяет системе S, следовательно, она не является крайней точкой.
Новый базис 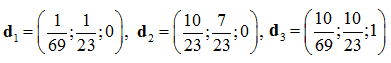 и матрица перехода от старого базиса к новому:
и матрица перехода от старого базиса к новому: 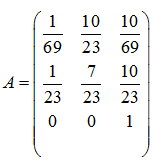 .
.
Избавимся от дробей, умножив матрицу A на 69. В результате получилась следующая матрица перехода: 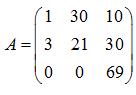 .
.
Далее выражаем координаты точки ![]() через
через ![]() :
:
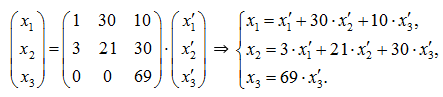
В итоге сформировалась новая задача в новой системе координат:
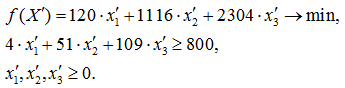
Окончательное решение: для минимальной стоимости в размере ![]() руб. необходимо
руб. необходимо 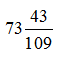 кг кукурузной,
кг кукурузной, 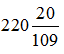 кг соевой и
кг соевой и 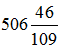 кг овсяной муки.
кг овсяной муки.
Выводы. Исследование задач оптимального управления предприятиями и задач о смесях показало справедливость следующих моментов. На примерах устанавливается, что в таких задачах естественны ситуации, в которых ограничения содержат группы неравенств, задающие некоторый многогранный конус. В этих случаях предлагается рассмотреть задачу в пространстве новых переменных. Базисом пространства должен быть набор векторов, который является образующей системой векторов для данного многогранного конуса. Оказывается, что на этом пути поиск решения может быть существенно упрощен. Предложена методика поиска образующей системы векторов. В заключение приводится пример, иллюстрирующий преимущества приведенного способа решения производственной задачам.
Список литературы
- Зангвилл У.И. Нелинейное программирование. – М.: Советское радио, 1973. – 312 с.
- Юдин Д.Б., Гольштейн Е.Г. Задачи и методы линейного программирования. — М.: Советское радио, 1961. – 493 с.
- Никайдо Х. Выпуклые структуры и математическая экономика. – М.: Мир, 1972. – 519 с.
- Севодин М.А., Семенова О.И. О конкурентных равновесиях в моделях экономического обмена растущего типа с ограничениями на цены// Вестник ИНЖЭКОНА, серия: Экономика. 2012. — Выпуск 6(57) — С. 103-106
- Гаврилова М.О., Новоселова Ю.В., Севодин М.А. Об одной модификации задачи размещения предприятий при планировании развития отрасли//»Фундаментальные исследования», 2016, №2, ч.1. – С. 92-96
- Таха Х.А. Введение в исследование операций. – М.: Издательский дом «Вильямс», 2005. – 912 с.
- Козловская Я.И., Севодин М.А. О положении равновесия в системах леонтьевского типа с ограничениями и неточными исходными данными//» Наука и бизнес: пути развития», 2015, №10(52). – С. 79-81
- Тищенко А.В. Линейная алгебра. Элементы аналитической геометрии. – М.: Финакадемия, 2009. – 116 с.