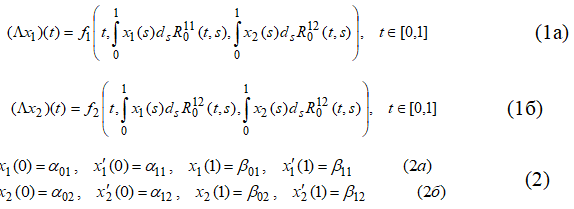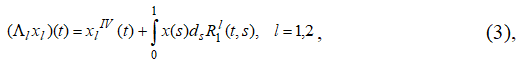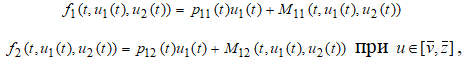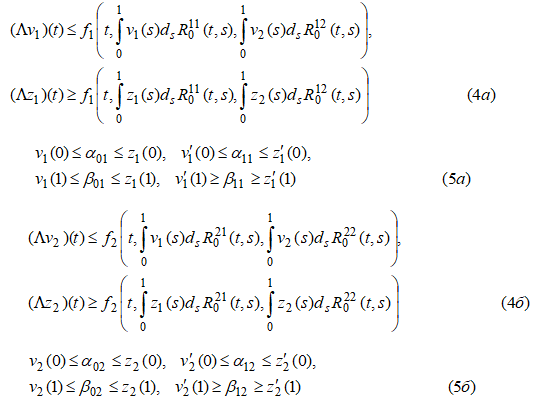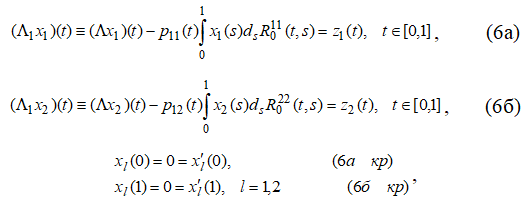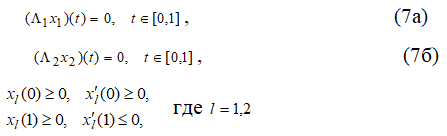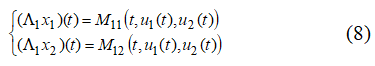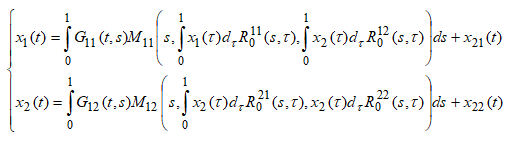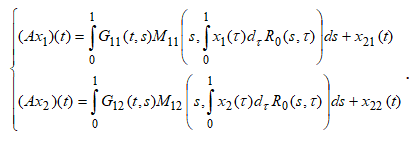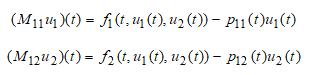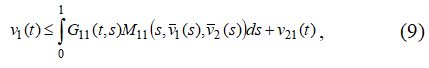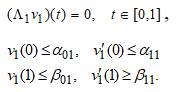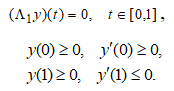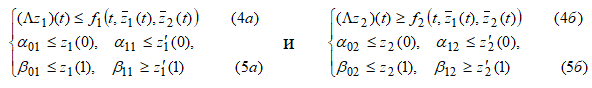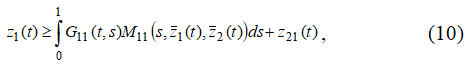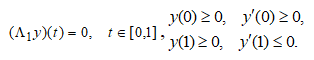Московский экономический журнал 12/2022 | Московский Экономический Журнал

PDF-файл статьи

Научная статья

Original article

УДК 517.999

doi: 10.55186/2413046X_2022_7_12_747

ОБ ОДНОЙ КРАЕВОЙ ЗАДАЧЕ ДЛЯ СИСТЕМЫ ФУНКЦИОНАЛЬНО-ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

ON A BOUNDARY VALUE PROBLEM FOR A SYSTEM OF FUNCTIONAL DIFFERENTIAL EQUATIONS

Пушкарев Герман Артурович, канд. ф.-м.н., доцент кафедры прикладной математики, Пермский национальный исследовательский политехнический университет, E-mail: gpushkariev@mail.ru

Воробьева Елена Юрьевна, ст. преподаватель кафедры прикладной математики, Пермский национальный исследовательский политехнический университет, E-mail: lena-vorobey@yandex.ru

Соколов Владимир Александрович, канд. ф.-м.н., доцент кафедры прикладной математики, Пермский национальный исследовательский политехнический университет, E-mail: sokolov.pstu@gmail.com

Pushkarev German Arturovich, associate professor of the department of applied mathematics, Perm national research polytechnic university, gpushkariev@mail.ru

Vorobyova Elena Urevna, senior lecturer department of applied mathematics, Perm national research polytechnic university, E-mail: lena-vorobey@yandex.ru

Sokolov Vladimir Alexandrovich, associate professor of the department of applied mathematics, Perm national research polytechnic university, sokolov.pstu@gmail.com

Аннотация. В статье рассматривается краевая задача для системы двух квазилинейных функционально-дифференциальных уравнений четвертого порядка. На основе схемы «квазилинеаризации» задача сводится к эквивалентной системе уравнений с изотонными операторами. Установлен признак существования решения нелинейной краевой задачи.

Abstract. The article considers a boundary value problem for a system of two quasi-linear functional differential equations of the fourth order. Based on the «quasi-linearization» scheme, the problem is reduced to an equivalent system of equations with isotonic operators. A sign of the existence of a solution to a nonlinear boundary value problem is established.

Ключевые слова: система функционально-дифференциальных уравнений, краевая задача, линейный ограниченный оператор, метод монотонных операторов

Keywords: system of functional differential equations, boundary value problem, linear bounded operator, method of monotone operators

Рассмотрим краевую задачу для системы квазилинейных функционально-дифференциальных уравнений (1а)

в следующих предположениях: операторы определены равенствами

где: функции измеримы в квадрате ; полная вариация 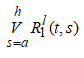суммируема на измеримы в квадрате полная вариация 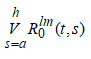суммируема на не убывают по s при почти всех функции удовлетворяет условиям Каратеодори: измеримы по t при всех и непрерывны по при почти всех

При указанных предположениях операторы определяемые равенствами (3), непрерывно действуют из пространства Соболева функций с абсолютно непрерывной производной третьего порядка в пространство суммируемых функций Поэтому под решением системы краевой задачи (1а,б)-(2а,б) будем понимать такую пару для которой равенства (1а,б) выполняются почти всюду (далее «п.в.») на .

Изучение краевой задачи (1а,б)-(2а,б) проведем на основе схемы квазилинеаризации», приведенной в работах [1], [2], [4]. Эта схема позволяет редуцировать задачу (1а,б)-(2а,б) к эквивалентной системе уравнений с изотонными операторами и в дальнейшем использовать следующее утверждение Тарского-Биркгофа-Канторовича [1].

Утверждение 1. [1],[3]. Пусть оператор где 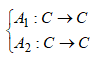изотонные, вполне непрерывные и существуют такие функции что 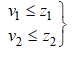и выполняются неравенства 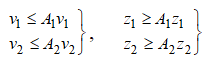и последовательные приближения начатые с и сходятся соответственно к «нижнему» и к «верхнему» решениям уравнения и эти решения таковы, что для любого решения имеют место неравенства

Пусть — некоторый порядковый интервал в пространстве L.

Будем говорить [1], что функция удовлетворяет условию если существует такая суммируемая на функция и такой оператор что

где оператор изотонный по 1-й переменной (при любой фиксированной 2-й переменной), а оператор

изотонный по 2-й переменной (при любой фиксированной 1-й переменной).

Теорема. Пусть выполнены условия:

1) существует такая пара функций что и выполняются неравенства

2) функция удовлетворяет условию с коэффициентом таким, что вспомогательная краевая задача

однозначно разрешима и ее функция Гри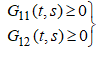на на а решение задачи

не принимает отрицательных значений на Тогда краевая задача (1а,б), (2) имеет решение удовлетворяющее неравенствам

Доказательство. Используя условие краевую задачу (1а,б), (2) запишем в следующем виде:

и пусть выполнены краевые условия (2). В силу однозначной разрешимости краевой задачи (6а,б), (6а.б кр), задача (8) эквивалентна системе уравнений

в пространстве С, где и — решения краевых задачи

Определим оператор равенствами

Оператор A является вполне непрерывным, так как операторы 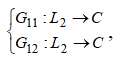определяемые равенствами 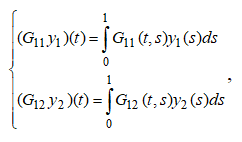вполне непрерывны [1]; операторы 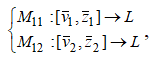определяемые равенствами

непрерывны в силу выполнения условий Каратеодори для функций и а операторы 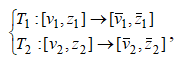т.е. 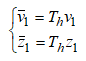определяемые равенствами 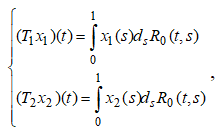ограничены. Операторы изотонные, так как функции Грина положительны в квадрате операторы являются изотонными операторами (соответственно по 1-й и по 2-й переменным), а операторы — изотонными.

Таким образом, мы провели редукцию задачи (1а,б), (2) к уравнению где — вполне непрерывный изотонный оператор.

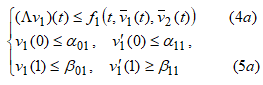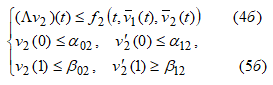Покажем, что из неравенств cледует выполнение неравенства а из неравенств cледует выполнение неравенства

Действительно, из неравенства (4а) имеем

В силу однозначной разрешимости задачи (6а), (6а,б кр) и положительности функции Грина в квадрате получим неравенство

где — решение краевой задачи

Введем обозначение: Несложно заметить, что удовлетворяет следующей задаче:

Так как решение задачи (7а) по условию не принимает отрицательных значений на то получим на т.е. Отсюда и из неравенств (9) имеем 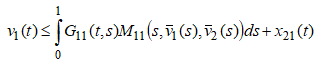или

Совершенно аналогично доказывается и неравенство

Аналогично можно показать, что из неравенств

cледует выполнение неравенства

Действительно, из неравенства (4а) имеем

где — решение краевой задачи

Введем обозначение: Несложно заметить, что удовлетворяет следующей задаче:

Так как решение задачи (7а) по условию не принимает отрицательных значений на то получим на т.е. Отсюда и из неравенства (10) имеем

Совершенно аналогично доказывается и неравенство т.е. неравенство

доказано.

Тогда по утверждению 1 имеем: последовательные приближения начатые и сходятся соответственно к «нижнему» и «верхнему» решениям уравнения эти решения принадлежат порядковому интервалу и для любого решения уравнения имеют место неравенства

Что и требовалось доказать.

Список источников

Канторович Л. В., Акилов Г. П. Функциональный анализ., 3-е изд. – М.:Наука, 1984. – 752 с.
Азбелев Н. В., Максимов В. П., Рахматуллина Л. Ф. Введение в теорию функционально-дифференциальных уравнений. М., Наука, 1991, — 278 с.
Азбелев Н. В., Рахматуллина Л. Ф. Абстрактное функционально-дифференциальное уравнение//Функционально-дифференциальные уравнения. Пермь, ППИ, 1987. Т.14, с. 3-11.
Г. А. Пушкарев, Е. Ю. Воробьева Разрешимость одной краевой задачи для дифференциального уравнения с отклонением аргумента./
Перспективы науки. Информатика, вычислительная техника и управление. Тамбов. — 2015 .— № 8(71).— С. 74-78.

References

Kantorovich L. V., Akilov, G. P. Functional analysis., 3 Izd. — M: Nauka, 1984. — 752 s.
Azbelev N. V., Maksimov, B. N., Rakhmatullina L. F. Introduction to the theory of functional differential equations. M., Nauka, 1991, — 278 C.
Azbelev N. V., Rakhmatullina L. F. Functional differential equations// Differential equations. 1978. T.14, № 5. C. 771-797.
Pushkarev G. A. , Vorobyova E. Yu. Solvability of a boundary value problem for differential th equations with deviation argument./
Prospects of science. Computer science, computer engineering and management. Tambov. — 2015 .— № 8(71).— S. 74-78.

Для цитирования: Пушкарев Г.А., Воробьева Е.Ю., Соколов В.А., Об одной краевой задаче для системы функционально-дифференциальных уравнений // Московский экономический журнал. 2022 . №12. URL: https://qje.su/ekonomicheskaya-teoriya/moskovskij-ekonomicheskij-zhurnal-12-2022-50/