УДК 528.914

Лебедев Петр Петрович,
доктор технических наук, профессор
Донцов Александр Владимирович,
доктор географических наук, профессор
Конокотин Николай Георгиевич
Лукьянова Татьяна Семёновна,
доктор географических наук, профессор
Государственный университет по землеустройству, г. Москва
Lebedev Petr Petrovich,
Doctor of Technical Sciences, Professor
Dontsov Aleksandr Vladimirovich,
Doctor of Geographical Sciences, Professor
State University if Land Use Planning, Moscow
ОПЫТ МОДЕЛИРОВАНИЯ КАРТОГРАФИЧЕСКОЙ ГЕНЕРАЛИЗАЦИИ
THE EXPERIENCE OF SIMULATION OF CARTOGRAPHIC GENERALIZATION
Аннотация
Предложен и опробован математический аппарат описания структуры географических карт математического моделирования и анализа картографической генерализации.
Abstract
Proposed and tested a mathematical apparatus describing structures maps of mathematical modeling and analysis of cartographic generalization.
Ключевые слова: вероятность совместного события, матрица вероятностей, энтропия, негэнтропия, структурная перестройка.
Keywords: the probability of the joint events, probability matrix, entropy, negentropy, restructuring
Рассматриваемый опыт моделирования картографической генерализации основан на описании структуры вероятностями наличия в парах соседних точек (смежных ячеек) i и j элементов из состава легенды или вероятностями совместных событий.
Вероятность совместного события pij=nij/n представляет собой долю смежных пар, сочетающих i j классы из состава классифицированной системы легенды карты, насчитывающей m классов в общем количестве пар позиций (точек, ячеек) пространства карты, дискретизированного посредством палетки или сканированием с шагом ∆x = ∆y по направлениям осей X и Y. Структура информации карты описывается, таким образом, матрицами ее подструктур Px и Py размером m х m, диагонали которых – это значения доли каждого класса смежных пар, сочетающих элементы каждого класса с самими собой или одноклассников pij, а другие, недиагональные значения pij – доли пар разноклассников, сочетающих каждый класс с каждым другим классном. Матрицы Px и Py являются численным выражением пространственных отношений между элементами, из которых образована структура информации карты, отражающим такие ее показатели как количество классов элементов, их относительные размеры, количество занимаемых ими контуров (контурность), а также относительную протяженность линий примыкания (границ) или смежности контуров. С их помощью можно по значениям pij ранжировать элементы (занимаемые ими площади), а по значениям pij оценивать степень взаимосвязи между ними, тем самым выявлять устойчивую, закономерную составляющую или ядро структуры. Кроме того, матрицей, ∆P= Px — Py можно оценивать симметрию (асимметрию) структуры, а матрицей Р = (Px + Py)/2 получать обобщенное описание структуры. Вычисленными по значениям матриц показателям удельного количества информации (бит), приходящегося на одну пару элементов, или энтропии H=∑mj∑mi log2pij можно измерять сложность структуры, в частности, Hx, Hy и H по по значениям трех матриц соответственно (Px, Py, P). Предложенный аппарат позволяет описывать не только состояние структуры картографической информации, но и, что важно ее изменения, которые учитываются в значениях pij матриц и соответственно H, тем самым моделировать генерализацию как структурное преобразование информации исходной карты. Проверку «работоспособности» аппарата можно показать на примере сравнения значений матриц Px, Py, P и энтропии Hx, Hy и H фрагмента на рисунке 1 и производного от него фрагмента (рис. 2), полученного в результате отбора небольшого контура А и сглаживания границ контуров.
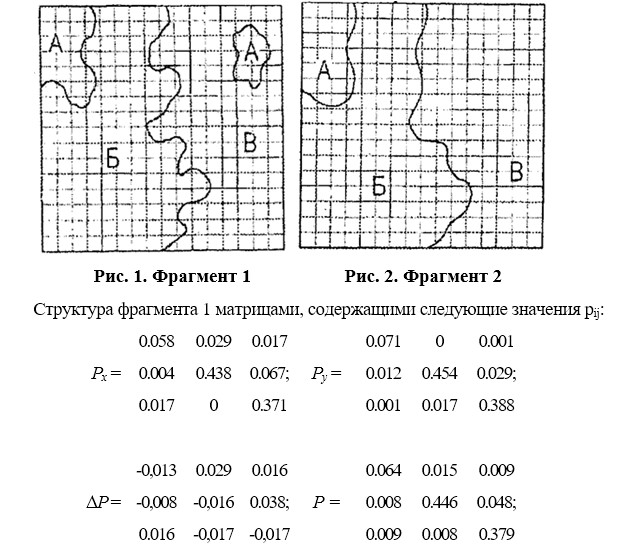
Энтропии структуры фрагмента, полученные по данным матриц Px, Py и P, соответственно равны Hx = 1.939; Hy=1,598 и H=1,846.
Структурные изменения фрагмента 2 отражены значениями матриц Px, Py, ∆Р, P и полученные в результате генерализации фрагмента 1 энтропий Hx, Hy и H:
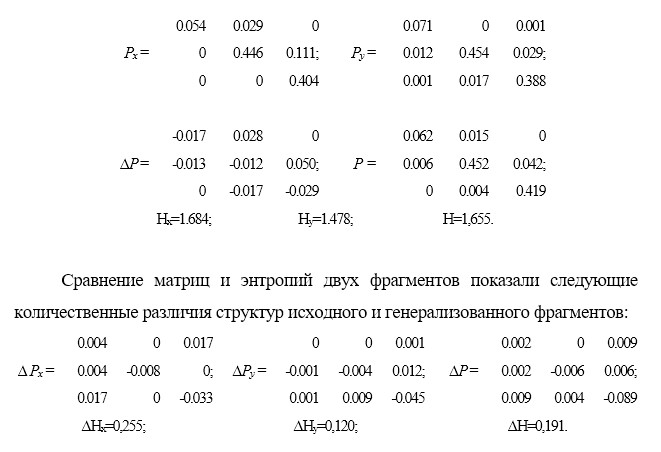
Кроме изменений в распределении классов элементов и отношений смежности между ними сравнительный анализ показал убыль сложности структуры. При этом эту убыль не следует понимать буквально, только как упрощение, поскольку генерализация — это не только и не столько механический отсев малоразмерных и малозначимых элементов, сколько научная и профессиональная перестройка структуры, позволяющая выделить в ней типичное, закономерное, подчеркнуть индивидуальное, особенное и ориентировать ее на определенные задачи. Сложность и ее показатель энтропия с точки зрения теории систем имеют обратную сторону — упорядоченность и негэнтропию. Поэтому структура, прошедшая процедуру научной и профессиональной перестройки, становится более осмысленной и целенаправленной или, определяя одним словом, упорядоченной, что выражается в приросте отрицательной энтропии или негэнтропии.
Результаты представленного опыта моделирования и картографической генерализации пока скромные, тем не менее они позволяют сделать вывод о правильности выбранного направления и методов исследования, и принципиальной возможности изучить количественные закономерности этого сложного и субъективного процесса проектирования, и составления географических карт. О сложности и субъективности генерализации говорит тот факт, что она в отличии от других картографических процессов автоматизирована только в отдельных ее видах и лишь частично. В частности, в цензовом отборе отдельных элементов и в исключении узловых точек границ контуров, внутренний угол между смежными дугами, которых почти равен 180°. Трудно поддаются алгоритмизации неформальное обобщение классификаций элементов и практически не поддаются — операции обобщения плановых очертаний площадных и линейных элементов.
Из проведенного опыта следует принципиально важный вывод о том, что процесс генерализации поддается математическому описанию и изучению на его основе как преобразования картографических структур и что в последствии, после установления закономерностей преобразования в зависимости от методов и приемов генерализации его (процесс) можно алгоритмизировать не частично, а целиком.
Литература:
- Лебедев П.П. Значение и опыт математического представления географической карты как целого. / Лебедев П.П. //Известия РАН. Серия географическая. 2010 №3
- Лебедев П.П. Структурный анализ картографической генерализации./ Лебедев П.П. // Землеустройство, кадастр и мониторинг земель. 2016 №6
- Методика создания цифровой геоморфологической карты Москвы./ Кошкарев А.В., Маркелов А.В., Маркелов Д.А., Некрасова Л.А., Самсонова С.Ю.//Геоморфология. — 2011. № 2. С. 55-65.
- Лебедев П.П. Генерализация как преобразование картографической структуры./ Лебедев П.П.// Известия высших учебных заведений. Геодезия и аэрофотосъемка.- 2007. № 1. С. 141-153.
References:
- Lebedev P.P. Value and experience of mathematical representation of a geographical map as a whole. Proceedings of the Russian Academy of Sciences. Geographic series. 2010 №3/
- Lebedev P.P. Structural analysis of cartographic generalization. Land management, cadastre and land monitoring. 2016 №6/
- Technique for creating a digital geomorphological map of Moscow. / Koshkarev AV, Markelov AV, Markelov DA, Nekrasova LA, Samsonova S.Yu.// Geomorphology. — 2011. № 2. P. 55-65.
- Lebedev P.P. Generalization as a transformation of the cartographic structure. / Lebedev PP. // News of higher educational institutions. Geodesy and aerial photography. — 2007. № 1. P. 141-153.


